【統計学入門（東京大学出版会）】第13章練習問題解答

東京大学出版会から出版されている統計学入門（基礎統計学Ⅰ）について第13章の練習問題の解答を書いていく。

本章以外の解答
13.1
- i)
- ii)
- iii)
- iv)
- v)
13.2
- i)
- ii)
- iii)
- iv)

本章以外の解答

本章以外の練習問題の解答は別の記事で公開している。
必要に応じて参照されたい。

13.1

i)

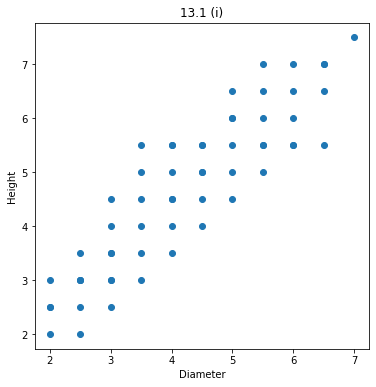
散布図を作成するPythonプログラムを次に示す。

import matplotlib.pyplot as plt

diameter = [
    2, 2, 2, 2, 2.5, 2.5, 2.5, 2.5, 2.5, 2.5, 3, 3, 3, 3, 3, 3, 3, 3.5,
    3.5, 3.5, 3.5, 3.5, 3.5, 4, 4, 4, 4, 4, 4, 4, 4.5, 4.5, 4.5, 4.5, 4.5, 4.5, 5, 5,
    5, 5, 5, 5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 6, 6, 6, 6, 6, 6.5, 6.5, 6.5, 6.5, 7,
]
height = [
    2, 2.5, 2.5, 3, 2, 2.5, 3, 3, 3, 3.5, 2.5, 3, 3, 3.5, 3.5, 4, 4.5, 3,
    3.5, 4, 4.5, 5, 5.5, 3.5, 4, 4.5, 4.5, 5, 5.5, 5.5, 4, 4.5, 5, 5, 5.5, 5.5, 6, 4.5,
    5, 5.5, 6, 6.5, 5, 5.5, 5.5, 6, 6.5, 7, 5.5, 5.5, 6, 6.5, 7, 5.5, 6.5, 7, 7, 7.5,
]

fig = plt.figure(figsize=(6, 6))
fig.patch.set_alpha(1)

plt.subplot(1, 1, 1)
plt.scatter(diameter, height)
plt.xlabel("Diameter")
plt.ylabel("Height")
plt.title("13.1 (i)")

上記のプログラムを実行すると、次の図が得られる。

f:id:nuka137:20201012072055p:plain

ii)

直径を $X_{i}$ 、その標本平均を $\bar{X}$ 、樹高を $Y_{i}$ 、その標本平均を $\bar{Y}$ とすると、標本回帰方程式、

$\begin{align} Y = \hat{\beta}_{1} + \hat{\beta}_{2} X \end{align}$

$\begin{align} \hat{\beta}_{1} = \bar{Y} - \hat{\beta}_{2} \bar{X} \end{align}$

$\begin{align} \hat{\beta}_{2} = \frac{ \sum (X_{i} - \bar{X})(Y_{i} - \bar{Y}) }{\sum (X_{i} - \bar{X})^{2}} \end{align}$

となる。

Pythonプログラム

import numpy as np

diameter = np.array([
    2, 2, 2, 2, 2.5, 2.5, 2.5, 2.5, 2.5, 2.5, 3, 3, 3, 3, 3, 3, 3, 3.5,
    3.5, 3.5, 3.5, 3.5, 3.5, 4, 4, 4, 4, 4, 4, 4, 4.5, 4.5, 4.5, 4.5, 4.5, 4.5, 5, 5,
    5, 5, 5, 5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 6, 6, 6, 6, 6, 6.5, 6.5, 6.5, 6.5, 7,
])
height = np.array([
    2, 2.5, 2.5, 3, 2, 2.5, 3, 3, 3, 3.5, 2.5, 3, 3, 3.5, 3.5, 4, 4.5, 3,
    3.5, 4, 4.5, 5, 5.5, 3.5, 4, 4.5, 4.5, 5, 5.5, 5.5, 4, 4.5, 5, 5, 5.5, 5.5, 6, 4.5,
    5, 5.5, 6, 6.5, 5, 5.5, 5.5, 6, 6.5, 7, 5.5, 5.5, 6, 6.5, 7, 5.5, 6.5, 7, 7, 7.5,
])

beta2 = np.sum((diameter - np.mean(diameter)) * (height - np.mean(height))) / np.sum((diameter - np.mean(diameter))**2)
beta1 = np.mean(height) - beta2 * np.mean(diameter)

print(f"y = {beta2} x + {beta1}")

を実行することにより、標本回帰係数 $\hat{\beta}_{1}, \hat{\beta}_{2}$ が求まり、標本回帰方程式が次のように得られる。

y = 0.9324473104749922 x + 0.7261717521233093

iii)

標本回帰方程式の傾き $\beta_{2}$ の検定を行う。帰無仮説を $\beta_{2} = 0.9$ 、対立仮説を $\beta_{2} \neq 0.9$ とする。

回帰残差 $\hat{e}_{i}$ 、標準誤差 $s.e. (\hat{\beta}_{2})$ は、

$\begin{align} \hat{e}_{i} = Y_{i} - \hat{\beta}_{1} - \hat{\beta}_{2} X_{i} \end{align}$

$\begin{align} s.e. ( \hat{\beta}_{2} ) = \frac{ \sqrt{ \sum \hat{e}_{i}^{2} / (n-2) } }{ \sqrt{ \sum (X_{i} - \hat{X})^{2} } } \end{align}$

で与えられ、

$\begin{align} t = \frac{\hat{\beta}_{2} - \beta_{2}}{s.e. (\hat{\beta_{2}})} \end{align}$

は自由度 $n-2$ のスチューデントのt分布に従う。

このため、

$\begin{align} -t_{0.025} \le t \le t_{0.025} \end{align}$

が成り立つとき、直径が1寸延びれば0.9尺だけ高くなる仮説が有意水準5%で棄却されない。

このことについてPythonプログラムを使って調べる。

import numpy as np
from scipy.stats import t

diameter = np.array([
    2, 2, 2, 2, 2.5, 2.5, 2.5, 2.5, 2.5, 2.5, 3, 3, 3, 3, 3, 3, 3, 3.5,
    3.5, 3.5, 3.5, 3.5, 3.5, 4, 4, 4, 4, 4, 4, 4, 4.5, 4.5, 4.5, 4.5, 4.5, 4.5, 5, 5,
    5, 5, 5, 5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 6, 6, 6, 6, 6, 6.5, 6.5, 6.5, 6.5, 7,
])
height = np.array([
    2, 2.5, 2.5, 3, 2, 2.5, 3, 3, 3, 3.5, 2.5, 3, 3, 3.5, 3.5, 4, 4.5, 3,
    3.5, 4, 4.5, 5, 5.5, 3.5, 4, 4.5, 4.5, 5, 5.5, 5.5, 4, 4.5, 5, 5, 5.5, 5.5, 6, 4.5,
    5, 5.5, 6, 6.5, 5, 5.5, 5.5, 6, 6.5, 7, 5.5, 5.5, 6, 6.5, 7, 5.5, 6.5, 7, 7, 7.5,
])

beta2 = 0.9324473104749922
beta1 = 0.7261717521233093
pred = beta1 + beta2 * diameter
e = height - pred
n = height.size

s = np.sum(e**2) / (n - 2)
se = np.sqrt(s)
beta2_se = se / np.sqrt(np.sum((diameter - np.mean(diameter))**2))

criteria = (beta2 - 0.9) / beta2_se
rejection = t.ppf(q=1-0.025, df=n-2)

print("Rejection: |t| > |{}|, Criteria: {}, {}".format(rejection, criteria, "Accept" if abs(criteria) < abs(rejection) else "Reject"))

上記のプログラムを実行すると、

Rejection: |t| > |2.0032407174966975|, Criteria: 0.5132092804206397, Accept

が得られ、直径が1寸延びれば0.9尺だけ高くなると言える。

iv)

iii)において、

$\begin{align} abs(\hat{e}_{i}^{2}) \gt 2 \cdot s.e. ( \hat{\beta}_{2} ) \end{align}$

を満たす標本が存在するか否かを確認する。

Pythonプログラム

import numpy as np
from scipy.stats import t

diameter = np.array([
    2, 2, 2, 2, 2.5, 2.5, 2.5, 2.5, 2.5, 2.5, 3, 3, 3, 3, 3, 3, 3, 3.5,
    3.5, 3.5, 3.5, 3.5, 3.5, 4, 4, 4, 4, 4, 4, 4, 4.5, 4.5, 4.5, 4.5, 4.5, 4.5, 5, 5,
    5, 5, 5, 5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 6, 6, 6, 6, 6, 6.5, 6.5, 6.5, 6.5, 7,
])
height = np.array([
    2, 2.5, 2.5, 3, 2, 2.5, 3, 3, 3, 3.5, 2.5, 3, 3, 3.5, 3.5, 4, 4.5, 3,
    3.5, 4, 4.5, 5, 5.5, 3.5, 4, 4.5, 4.5, 5, 5.5, 5.5, 4, 4.5, 5, 5, 5.5, 5.5, 6, 4.5,
    5, 5.5, 6, 6.5, 5, 5.5, 5.5, 6, 6.5, 7, 5.5, 5.5, 6, 6.5, 7, 5.5, 6.5, 7, 7, 7.5,
])

beta2 = 0.9324473104749922
beta1 = 0.7261717521233093
pred = beta1 + beta2 * diameter
e = height - pred
n = height.size

s = np.sum(e**2) / (n - 2)
se = np.sqrt(s)

over_2se = np.abs(e) > 2 * se
if over_2se.sum() > 0:
    print("Exist")
    over_diameter = diameter[over_2se]
    over_height = height[over_2se]
    for d, h in zip(over_diameter, over_height):
        print("({}, {})".format(d, h))
else:
    print("Not exist")

より、

Exist
(3.5, 5.5)

が得られ、(直径, 樹高) = (3.5, 5.5) の標本が標本回帰直線から2s.e.以上外れた樹木であるとわかる。

v)

ii)で得られた結果を使い、直径8寸のときの樹高を推定すればよい。

y = 0.9324473104749922 x + 0.7261717521233093

Pythonプログラム

beta2 = 0.9324473104749922
beta1 = 0.7261717521233093
pred = beta1 + beta2 * 8

print(pred)

により、

8.185750235923248

が得られる。

13.2

i)

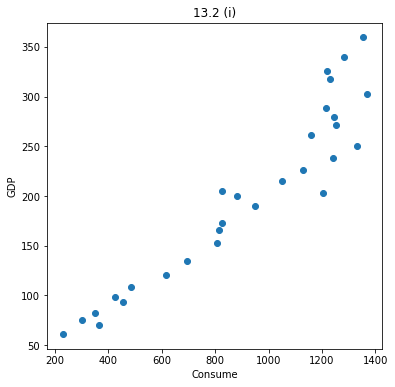
散布図を作成するPythonプログラムを次に示す。

import numpy as np
import matplotlib.pyplot as plt

consume = np.array([
    229, 367, 301, 352, 457, 427, 485, 616,
    695, 806, 815, 826, 951, 1202, 881, 827, 1050, 1127, 1241,
    1330, 1158, 1254, 1243, 1216, 1368, 1231, 1219, 1284, 1355,
])
gdp = np.array([
    61.2, 70.0, 74.9, 82.8, 93.6, 98.5, 108.8, 120.1,
    135.1, 152.5, 165.8, 173.0, 189.9, 202.6, 199.7, 205.0, 214.9, 226.3, 238.1,
    250.7, 261.4, 271.0, 279.3, 288.4, 303.0, 317.3, 325.7, 340.3, 359.5,
])

fig = plt.figure(figsize=(6, 6))
fig.patch.set_alpha(1)

plt.subplot(1, 1, 1)
plt.scatter(consume, gdp)
plt.xlabel("Consume")
plt.ylabel("GDP")
plt.title("13.2 (i)")

上記プログラムを実行すると、次の図が得られる。

f:id:nuka137:20201012082849p:plain

ii)

実質GDPを $X_{i}$ 、銅消費量を $Y_{i}$ としたとき、標本回帰方程式、

$\begin{align} \log Y = \hat{\beta}_{1} + \hat{\beta}_{2} \log X \end{align}$

$\begin{align} \hat{\beta}_{1} = mean(\log Y) - \hat{\beta}_{2} \cdot mean(\log X) \end{align}$

$\begin{align} \hat{\beta}_{2} = \frac{ \sum (\log X_{i} - mean(\log X) )(\log Y_{i} - mean(\log Y) ) }{\sum (\log X_{i} - mean (\log X) )^{2}} \end{align}$

となる。

Pythonプログラム

import numpy as np

gdp = np.array([
    61.2, 70.0, 74.9, 82.8, 93.6, 98.5, 108.8, 120.1,
    135.1, 152.5, 165.8, 173.0, 189.9, 202.6, 199.7, 205.0, 214.9, 226.3, 238.1,
    250.7, 261.4, 271.0, 279.3, 288.4, 303.0, 317.3, 325.7, 340.3, 359.5,
])
consume = np.array([
    229, 367, 301, 352, 457, 427, 485, 616,
    695, 806, 815, 826, 951, 1202, 881, 827, 1050, 1127, 1241,
    1330, 1158, 1254, 1243, 1216, 1368, 1231, 1219, 1284, 1355,
])

consume_log = np.log(consume)
gdp_log = np.log(gdp)

beta2 = np.sum((gdp_log - np.mean(gdp_log)) * (consume_log - np.mean(consume_log))) / np.sum((gdp_log - np.mean(gdp_log))**2)
beta1 = np.mean(consume_log) - beta2 * np.mean(gdp_log)

print(f"log(y) = {beta2} log(x) + {beta1}")

を実行することにより、標本回帰係数 $\hat{\beta}_{1}, \hat{\beta}_{2}$ が求まり、標本回帰方程式が次のように得られる。

log(y) = 0.966869094731703 log(x) + 1.6898916241200759

iii)

実質GDPが4%/年で増加すると仮定すると、2000年の銅消費量 $Y_{2020}$ は、

$\begin{align} Y_{2000} = Y_{1988} \cdot (1 + 0.04 \hat{\beta}_{2}) \cdot (2000 - 1988) \end{align}$

であるから、ii)の結果を利用してPythonプログラム

consume_1988 = 1355
beta_2 = 0.966869094731703
pred = consume_1988 * (1 + beta_2 * 0.04)**(2000-1988)
print(pred)

により、2000年の銅消費量、

2136.457480272669

が得られる。

iv)

標本回帰方程式の傾き $\beta_{2}$ の検定を行う。帰無仮説を $\beta_{2} = 1$ 、対立仮説を $\beta_{2} \neq 1$ とする。

回帰残差 $\hat{e}_{i}$ 、標準誤差 $s.e. (\hat{\beta}_{2})$ は、

$\begin{align} \hat{e}_{i} = \log Y_{i} - \hat{\beta}_{1} - \hat{\beta}_{2} \log X_{i} \end{align}$

$\begin{align} s.e. ( \hat{\beta}_{2} ) = \frac{ \sqrt{ \sum \hat{e}_{i}^{2} / (n-2) } }{ \sqrt{ \sum (\log X_{i} - mean(\log X) )^{2} } } \end{align}$

で与えられ、

$\begin{align} t = \frac{\hat{\beta}_{2} - \beta_{2}}{s.e. (\hat{\beta}_{2})} \end{align}$

は自由度 $n-2$ のスチューデントのt分布に従う。

このため、

$\begin{align} -t_{0.025} \le t \le t_{0.025} \end{align}$

が成り立つとき、銅消費量のGDP弾性値が1であるという仮説が有意水準5%で棄却されない。

このことについてPythonプログラムを使って調べる。

import numpy as np
from scipy.stats import t

gdp = np.array([
    61.2, 70.0, 74.9, 82.8, 93.6, 98.5, 108.8, 120.1,
    135.1, 152.5, 165.8, 173.0, 189.9, 202.6, 199.7, 205.0, 214.9, 226.3, 238.1,
    250.7, 261.4, 271.0, 279.3, 288.4, 303.0, 317.3, 325.7, 340.3, 359.5,
])
consume = np.array([
    229, 367, 301, 352, 457, 427, 485, 616,
    695, 806, 815, 826, 951, 1202, 881, 827, 1050, 1127, 1241,
    1330, 1158, 1254, 1243, 1216, 1368, 1231, 1219, 1284, 1355,
])

consume_log = np.log(consume)
gdp_log = np.log(gdp)


beta2 = 0.966869094731703
beta1 = 1.6898916241200759
pred = beta1 + beta2 * gdp_log
e = consume_log - pred
n = consume_log.size

s = np.sum(e**2) / (n - 2)
se = np.sqrt(s)
beta2_se = se / np.sqrt(np.sum((gdp_log - np.mean(gdp_log))**2))

criteria = (beta2 - 1) / beta2_se
rejection = t.ppf(q=1-0.025, df=n-2)

print("Rejection: |t| > |{}|, Criteria: {}, {}".format(rejection, criteria, "Accept" if abs(criteria) < abs(rejection) else "Reject"))

上記を実行すると、

Rejection: |t| > |2.0518305164802833|, Criteria: -0.7251395116305018, Accept

が得られ、銅消費量のGDP弾性値が1であるといえる。