【機械学習】バイアスとバリアンスのトレードオフ
毎回悩むことの多いので、モデルの予測誤差を構成するバイアス(偏り)とバリアンス(分散)についてまとめる。
平均二乗誤差(MSE)
機械学習において、モデルの予測誤差を測る指標の1つとして 平均二乗誤差(MSE) がある。
MSEは、真の値を 、モデルの予測値を
として次のように表される。
バイアス-バリアンス分解
平均二乗誤差の式を変形すると、
のように2つの項に分解できる。 第1項が バイアス、第2項が バリアンス であり、モデルの予測誤差をバイアスとバリアンスに分解することを バイアス-バリアンス分解 と呼ぶ。
バイアス、バリアンスの意味
バイアスとバリアンスの意味を考える。
バイアスは、
で表される。
モデルの予測値 の期待値と真の値
の差が小さいほど、バイアスが小さくなる。
すなわち、データに対するモデルのあてはまりの良さを測定していると言え、バイアスが小さいほど学習に使用したデータにより適合していると言える。
バリアンスは、
で表される。
バリアンスの名前の通り、モデルの予測値に対する分散を示している。
モデルの予測値 とその期待値の差が小さいほどバリアンスが小さくなることから、バリアンスが小さいモデルは安定していると言える。
バイアス・バリアンスのトレードオフ
学習に使用するデータがノイズを含んでいる場合を想定する。
バイアスが小さくなるように(よりデータに適合するように)モデルを構築した場合、そのモデルはデータのノイズに対しても適合していることになる。 このため、小さいデータの値変動(ノイズ)に対してモデルの予測結果が不安定になりがちであり、バリアンスが大きいモデルと言える。
バリアンスが小さくなるように(データの値変動に対して無頓着な)モデルを構築した場合、モデルの予測結果は安定する一方で、そのモデルはデータの特徴を十分に捉えきれていないものになる。 このためモデルはデータに対して適合していないことになり、バイアスが大きくなる。
ここまでの議論により、バイアスとバリアンスの両方を同時に小さくすることはできず、互いにトレードオフの関係にあることがわかる。 このことを バイアス・バリアンスのトレードオフ 呼ぶ。
バイアス・バリアンスのトレードオフを確認するプログラム
実際にバイアス・バリアンスのトレードオフを確認するため、次のようなPythonプログラムを作成した。 このプログラムでは、sin曲線にノイズを加えた30個の学習データに対して1次・3次・10次・20次の多項式をfitさせ、バイアスとバリアンスがそれぞれの場合についてどのような値を取るかを確認する。
import numpy as np import matplotlib.pyplot as plt from math import pi np.random.seed(0) # Prepare data. (2*sin(x) + noise) X_train = np.linspace(0, 1, 30) y_train = 1.0 * np.sin(X_train * 2 * pi) + np.random.rand(*X_train.shape) - 0.5 # Predict with polynomial function. def predict(X, y, degree): w = np.polyfit(X, y, degree) f = np.poly1d(w) y_pred = f(X_train) return y_pred degrees = [1, 3, 10, 20] y_predicts = [] for deg in degrees: y_predicts.append(predict(X_train, y_train, deg)) # Draw train data and predict. fig = plt.figure(figsize=(12, 12)) fig.patch.set_alpha(1) for i, (deg, y_pred) in enumerate(zip(degrees, y_predicts)): plt.subplot(2, 2, i+1) plt.plot(X_train, y_train, ".", X_train, y_pred, "-") plt.title(f"degree={deg}") plt.xlabel("X") plt.ylabel("y") # Calculate bias and variance. biases = [] variances = [] for i, (deg, y_pred) in enumerate(zip(degrees, y_predicts)): biases.append(np.mean((y_train - y_pred)**2)) variances.append(np.mean((y_pred - np.mean(y_pred))**2)) # Draw biases and variances. fig = plt.figure(figsize=(6, 6)) fig.patch.set_alpha(1) bar_1 = plt.bar(np.arange(len(degrees)), biases, tick_label=degrees, width=0.3) bar_2 = plt.bar(np.arange(len(degrees)) + 0.3, variances, tick_label=degrees, width=0.3) plt.xlabel("degree") plt.legend((bar_1, bar_2), ("Bias", "Variance"))
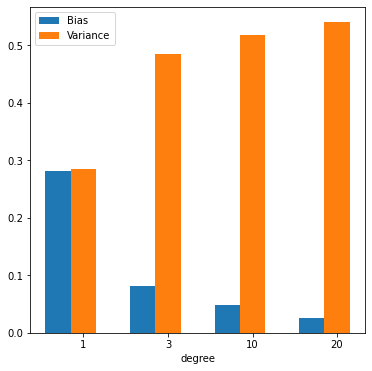
上記のプログラムを実行すると、最初に学習データと学習データに対してfitさせた多項式の図が表示される。 ノイズ成分からの影響が少なく、学習データの特徴をうまく捉えることに成功しているのは3次の多項式モデルであると言える。 一方で多項式の次数が10次や20次にもなると、学習データのノイズを拾うようになる。
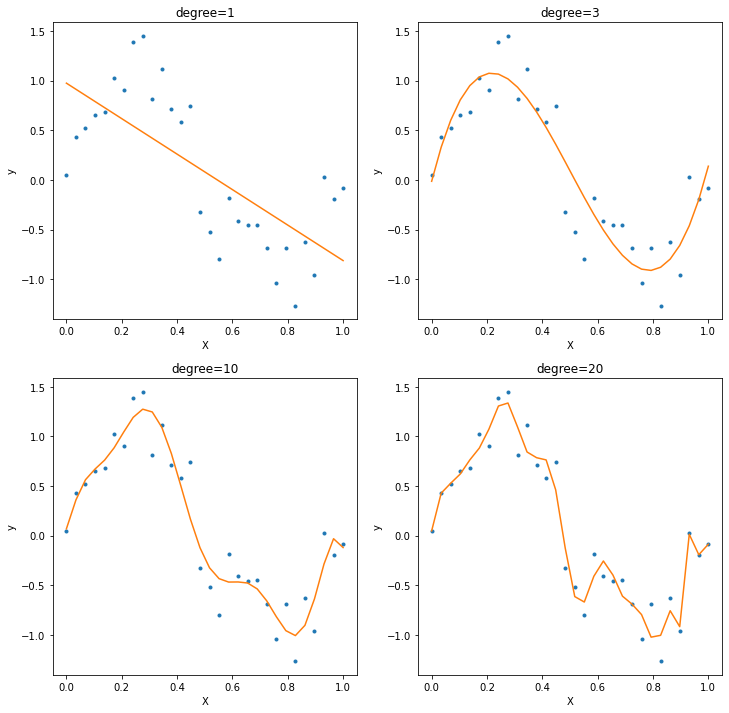
2つ目に出力される図は、各多項式の次数に対してバイアスとバリアンスの値をグラフにしたものである。 次数を増やすことにより、バイアスが減少していく一方でバリアンスが増加していくことがわかる。 この例からも、バイアスとバリアンスを両方同時に小さくできないこと(バイアス・バリアンスのトレードオフ)が確認できた。