2022-03-22

【合格体験談】JDLA Deep Learning for ENGINEER 2022 #1（E資格）

資格

2022/2/19にE資格と呼ばれるAIの資格試験「JDLA Deep Learning for ENGINEER 2022 #1」を受験してきました。結果としては合格でしたが、今後同じようにE資格を受験される方の参考になればよいと思い、合格のために私が行ってきたことを簡単にまとめたいと思います。

前提

E資格を受験することに決めたときの私の知識について書きます。

AI関連の資格
- 昨年の同時期に統計検定2級合格
数学に関する知識
- 現代数理統計学の基礎を第1章～第8章まで2回通した
- 統計検定1級に向けて勉強を進めていた（勉強時間が足りないと感じ、2021年は受験を見送った）
AIに関する知識
- 専用ハードウェア向けのAI学習高速化やMLOpsに関わっているため、開発・運用環境（特にGPU関連）に関しては知識あり
- 上記の業務の中でAIに関連する基本的な知識や理論は習得済み
- ゼロつくや MLPシリーズの深層学習本は5年くらい前に読んだが、完全に理解しているかと言われるとそうではない
- Kaggleでコンペに参加した経験が複数回あり、基本的な機械学習や深層学習の知識やアルゴリズム、実装経験あり

試験結果

受験費用が高額であることと次回（2022 #2）からシラバスが変わることから1回で合格したいと思い、集中して勉強しました。なんとしても1発合格したいというプレッシャーもあり、具体的に計測していませんが勉強時間は合計で100時間を超えている思います。

試験前は過去問がなくて問題レベルがわからないため、やや不安なところもありました。実際の試験では想定していた難易度よりもやや低めで、最後の問題を解き終わった段階で20分近く余りました。回答に不安がある問題の見直しも十分に行えたので、統計検定2級の時よりも合格の手ごたえがありました。ただ試験開始直後はPC操作に慣れず（特に電卓が使いにくい）、かなり焦りました。試験問題の内容は規約上詳しく書くことはできませんが、以降で紹介する黒本と例題集の範囲で十分に網羅できており、この2つを重点的に勉強しておけば合格はほぼ確実かと思います。

試験結果の詳細は次の通りでした。

分野	得点率	出題量内訳
応用数学	100%	10%
機械学習	89%	35%
深層学習	94%	50%
開発環境	100%	5%

6割くらいが合格ラインと言われる中で十分な得点率（90%超え）を取得できました。出題量内訳はこちらの情報を参考にしましたが、出題傾向が変わっているためあくまで参考程度の数値となります。試験終了後のためなんとでも言えますが、もう少し勉強の手を抜いて他のことに時間を使ってもよかったかなと思いました。 Twitterで6割に満たない得点率でも合格報告している人も見かけたので、合格ラインも想定より高くなさそうな感じでした。

勉強したこと

前提のところで書きましたが、AIや数学の基礎的な知識や理論は理解していたので、シラバスの範囲で知識が不足している部分を問題集や例題集で洗い出して勉強する方針で進めました。類題もいくつか出題されるため、問題集や例題集を仕上げることが合格に直結すると考えます。

徹底攻略ディープラーニングE資格エンジニア問題集

黒本と呼ばれている問題集です。 E資格向けの問題集としては、執筆時点で本書しか存在しないようで、本書はE資格を受ける人にとって必携かと思います。実際に私の場合も、E資格に向けての勉強はほとんどこれだけで済ませました。

3回以上繰り返して解き、最終的にはすべての問題に回答できるようにしました。もちろん何度も問題を解いていくと過学習気味になるため、数式の導出も含めて問題集の解説で取り扱っている内容も理解するようにしました。用語を丸暗記するのではなく、用語と周辺知識を結びつけて理解することが重要だと思います。 E資格の合格が目的ではなくE資格受験で得た知識を業務に活かしたい場合には、応用力を身につけるためにも丸暗記は避けるべきでしょう。解説がわかりづらい部分や「論文を参照」と書いている部分については、Web上の記事がとても参考になりました。

付属の模試1回分は問題集を2周した段階で解きましたが、初見で9割近く取れたので本番よりもやや簡単めの難易度に設定されていると思います。試験直前に解き、自信をつけた状態で本番に臨むと良いかと思います。

E資格に役立った本書ですが、注意点もあります。網羅範囲は本書が発行された時点のものであり、次回（2022 #2）以降は本書だけでシラバスの範囲を網羅できない可能性が高いです。将来的に新シラバスに対応した改訂版が発売される可能性が高いと思いますが、現時点で発行されているものを購入予定の方は注意しましょう。

AI STANDARD

ai-std.standard-dx.com

会社のお金でE資格を受験したため、会社で利用できる唯一のJDLA認定プログラム「株式会社STANDARD」を利用しました。機械学習、深層学習、E資格対策（例題集）の3本立てで、それぞれ最後に修了試験があります。ある程度事前知識があったので、講座自体は1回流し読みする程度で修了試験は一発合格でした。講座の内容を理解していれば合格は難しくないでしょう。

E資格の試験対策としては、黒本と同様に例題集のすべての問題に回答できるまで繰り返し解きました。問題の解説が不十分なところが多かったため、必要に応じてWeb上の記事を参照して納得するまで調べました。

感想とまとめ

高額な受験費用とシラバス変更の影響で1発合格しなければというプレッシャーがあったE資格ですが、無事合格できてよかったです。 E資格の勉強を通してAIに関する知識が受験前よりも増え、エンジニアとして次のステップに進むための地盤を固められたと思います。

今後は数理統計の観点からAIを理解するために統計検定1級の勉強に注力しつつ、業務範囲が広がったことからAI以外の知識習得にも力を入れていこうと思います。 JDLAによる認定資格としてAIのビジネス適用に焦点を置いた G検定もありますが、こちらは内容的にエンジニアよりもジェネラリスト向けの内容ということでskipしようかと思います。

E資格は資格ビジネスとか取得しても意味がないと言われることもありますが、個人的にはこれについて否定的な意見を持っています。たしかにJDLA認定プログラムや試験の価格を考えるとこの主張に対して理解できる部分もあります。しかしE資格取得に向けて勉強したことで得た知識は、今後もAIに関わっていくエンジニアとしても間違いなく役立つと感じています。実際E資格を受験しなければ、強化学習や深層学習で使われるモデルの詳細について勉強する機会はもう少し先になっていたと思います。

個人的に資格試験は合格することを目的とするのではなく、試験勉強で得た知識を業務などでどのように活かしていくかを考えながら勉強するのがよいと思っています。その意味でE資格は、AIに関する幅広い知識を得て次のステップに進むための良い資格であると思いました。

2021-11-07

【OSS開発】「Optuna V3開発スプリント #1」に参加してきました

OSS開発機械学習 Python

2021/10/31に開催された、Optuna開発者主催の開発スプリントに参加してきましたので、簡単に参加報告します。

optuna.connpass.com

イベントの概要

OptunaはML/DLのモデル開発はもちろんのこと、JVMのパラメータチューニングや物質の結晶構造解析など幅広く適用できる、ハイパーパラメータ自動最適化ツールです。現在のOptunaのバージョンはV2ですが、V3に向けたロードマップが示されるなど開発が進められています。今回開催された開発スプリントは、Optuna V3リリースに向けた機能開発を目的としていました。

イベント中のコミュニケーションはすべてDiscord上で進められ、テキストでやり取りしながら必要に応じてマイクやカメラをオンにしてVoiceチャットで開発に関して議論する流れになります。私は残念ながらマイクやカメラが利用できない環境での参加となり、テキストのみのコミュニケーションになってしまい残念でした。しかし、開発への支障はまったくなかったため、マイクやカメラが利用できないからという理由で参加を見送る必要はないでしょう。また、実際にGitHub上でPull Requestを送るまで開発者から丁寧にフォローがあり、これまでOptunaの開発を行なったことがない人でもモチベーションさえあれば問題なく参加できると思います。

イベントのスケジュール

開発スプリントは1日開催でした。過去に参加した scikit-learnの開発スプリントは2日〜3日の開催であったことを考えると、かなり短期間のスプリントです。開発スプリントは次のようなスケジュールで進み、開催期間中はほぼ開発に時間が割かれました。

時間	内容
10:00 - 10:30	開発スプリント、V3に向けた開発内容の説明、自己紹介
10:30 - 17:50	開発（途中自由に休憩、ランチ用のDiscordチャンネルが開設）
17:50 - 18:00	開発者から開発スプリント内での成果共有
18:00 -	オンライン懇親会（未参加）

開発内容

V3の開発タスクとして取り上げられていたのは以下のようなものでした。

インターフェースの整備
各種機能の安定性向上
Deprecated機能の削除
チュートリアル追加

具体的なタスクは、v3というラベルがついたIssue から選ぶことになります。タスクはどれも興味深いものでしたが、せっかく開発スプリントに参加していることもあり、過去に取り組んだドキュメントの作成タスクではなく開発系のタスクに取り組もうと思っていました。そして選んだのが、非推奨となった機能の削除というIssueです。このIssueは次の3つのタスクから構成されていました。

Deprecated機能のリストアップと削除機能の洗い出し
洗い出した削除機能の削除
@deprecated デコレータのリファクタリング

3つ目のタスクは、Issueでは Document @deprecated decorator と書いてありました。最初は @deprecated デコレータドキュメント化するのかと思っていましたが、いまひとつ進め方がわからなかったので開発者に聞いてみたところ、@deprecated のリファクタリングを意味していると教えてもらいました。不明瞭なタスクは、事前に確認しておくとスムーズに進められるよい例でした。

開発成果

ドキュメントや簡単なバグ修正などで過去にOptunaへコントリビュートしたことはありましたが、しばらく開発から離れていたこともあって開発環境の構築から始めました。また、選んだIssueが複数のタスクから構成されていることもあり、結局このIssueを対応するだけで1日使ってしまいました。途中でCIのエラーが取れずに悩んでしまう場面もありましたが、Optunaの開発者からフォローいただいたことで全体的にスムーズにタスクを進めることができたと思います。

作成したPull Requestは3つ（#3057、#3064、#3065）で、1つは開発スプリント中にマージされました。残りの2つはこの記事執筆時点でマージされていませんが、方針はほぼほぼ決まってプロトタイプも完成したため、あとはレビューやCIを通すのとクリーンアップするのみです。

次回について

V3に向けて開発を加速化してきていることもあり、今後も今回のような開発スプリントを月1回のペースで開催するようです。すでに次回の開催も決まっています。

optuna.connpass.com

オープンソースプロジェクトにコントリビュータとして参加できるよい機会ですので、Optunaの開発に興味のある方は参加してみるとよいかもしれません。私も都合があうときはまた参加してみたいと思います！

最後になりますが、このような貴重な場を設けていただき、かつ開発スプリント中にフォローしていただいたOptuna開発者のみなさまに感謝いたします。

2021-06-20

【合格体験談】統計検定2級

資格統計学

報告するのが遅くなりましたが、ちょうど年度変わりである2021/3/31に統計検定2級（CBT）に合格しました。統計学が機械学習や深層学習といったAI領域の技術の基礎ということもあり、統計検定の受験者数は年々増加しているようです。

統計検定2級は、資格試験の中では標準的な難易度に分類されるようです。大学で統計学を学んだ方であれば難なく取得できる資格であると思いますが、大学で統計学を学んでいなかった私はそれなりに勉強する必要がありました。そこで、これから統計検定2級を受験しようと考えている人向けに、統計検定2級に合格するために私が勉強したことを紹介したいと思います。

なぜ統計検定を受けようと思ったか

仕事で機械学習や深層学習のプロジェクトにかかわる中で、機械学習の論文や各種機械学習向けのライブラリで用意されているアルゴリズムを理解する必要が出てきました。これまでは知らないアルゴリズムが出てくるたびに本やWeb記事で調べることで対応していましたが、場当たり的であったために理解したようなしていないような感じでした。

基礎を固めるために機械学習界隈では非常に有名なPRML本を手に取って読み始めてみたのですが、バックグラウンドのない統計学の基礎知識が要求されるために100ページ足らずで挫折してしまいました。そこで統計学の知識をつけるために、東京大学出版会から出版されている統計学入門（基礎統計学Ⅰ）を読んだりして統計学の勉強を進めていくうちに統計検定というものを知りました。

今まで資格試験についてはあまり興味がなかったのですが、統計検定の範囲を見て体系的に学ぶには資格取得を目指すのもありだと思いました。これが統計検定を受けようと思ったきっかけです。

前提

最初に統計検定2級を受験することを決めたときの私の前提知識や背景などを書いておきます。

統計学に関する知識
- 平均、分散、信頼区間などの基礎知識はあった
- 確率分布や検定についての知識はなかった
数学について
- 大学では物理学を専攻していたため、大学数学に関してはある程度素養があった
- 大学院卒業後は微積や線形代数にほとんど触れていなかったため、部分積分すらも忘れていた
資格試験について
- 会社に入ってから資格試験を1度も受けていなかったため、試験というものに対してかなりのブランクがあった

このようにしばらく数式を扱っていなかったことと、統計学に関する知識がほぼない状態であったので、それなりに試験対策する必要がありました。

勉強したこと

ここからは統計検定2級に向けて勉強したことを書いていきます。最初は手探り状態であったこともあり、資格取得を目指すのであればもっと効率的な方法があったと感じています。

そしてここで紹介している方法は、ほかのすべての人にとって最適な方法とも限りません。これから統計検定2級に向けて勉強しようと考えている人は、あくまで参考程度に見てもらえればと思います。

統計学入門（基礎統計学Ⅰ）

言わずと知れた統計学の名著です。統計学についての基礎知識を得るため、本書を読みながら章末の問題を解きました。確率分布や検定あたりはまったく知らなかったため、統計学の考え方に慣れるまでが大変でしたが、この本の章末の問題を解くことで、統計学に対する理解が定着していきました。

理解を深めるために、問題の解答をまとめたりPythonプログラムで再現させたりしていました。このおかげで統計学に対する理解は深まった一方で、統計検定2級を取得することを目的とするならここまでやらなくてもよいかなと思いました。統計検定2級を取得することを目的とするなら、本書を1～2回読んだ後は過去問演習に移行してゴリゴリ問題を解いていくのが早道だと思います。

なお、統計検定2級で頻出の分散分析は本書の範囲外となっているため、別の教材などで勉強する必要があります。一方本書に関しては、数学的な素養（高校数学レベル）がない人が読むのは難しいという話もありますので、そのような方は次の「統計学の時間」から勉強を始めるのがよいと思います。

統計学の時間

正直なところ、統計検定2級の取得を目指すのであれば、このサイトにある内容を理解して演習問題と過去問をこなすだけで十分だと思いました。私も試験直前はこのサイトにある演習問題を一通り解きつつ過去問を解いて、理解が不十分なところをこのサイトで知識を補うことを繰り返していました。

試験対策としては、「統計学入門（基礎統計学Ⅰ）」よりもおすすめできます。網羅範囲も統計検定2級を意識しているようで、過去問に出てきた話題は難問を除いてほぼ網羅されていました。統計検定2級の解説記事を書いてあることからも統計検定2級を意識していることがわかります。

日本統計学会公式認定統計検定 2級公式問題集[2017〜2019年]

いわゆる過去問です。試験2週間くらい前は仕事が終わった後に時間を取って過去問を解き、理解できていなかった部分は「統計学の時間」で補っていました。

解説がきちんと理解できて、収録されている6回分について時間を測って8割～9割取れるようになるまで繰り返せば合格は目前だと思います。私は6回のテストすべてについて3回解き、最終的に9割正解くらいになっていました。

試験当日

CBTでの受験のため、いつでも受けられるという自由度の高い試験であるのにもかかわらず、久しぶりの試験ということでかなり緊張しました。実際に試験を開始したら、今まで勉強してきた内容がすぐに出てこなくて焦りました。このような試験では、試験慣れも合否に大きく影響を与えると思いました。

試験内容については守秘義務もあり深くは説明できませんが、おおよそ過去問と同じくらいかやや難しい印象がありました。紙媒体方式では7割で合格であるのに対してCBTでは6割で合格であることから、難易度が調整されているのかもしれません。また計算用紙も配られるのですが、純粋な紙ではないためその点もやりづらかったです。

電卓は持ち込んで正解でした。電卓はカシオ製のものを事前に購入しておき、過去問を解くときに使用して使い方に慣れておきました。

電卓を使うことで計算ミスなどを防げるので、持ち込むことをおすすめします。ただし関数電卓のような高機能な電卓は持ち込み不可であるため注意が必要です。上記のカシオ製の電卓は持ち込み可でした。

当日は時間配分がうまくいき、一通り最後まで解いたところで時間があまりました。あまった時間は自信がなかった部分を見直したり、その場ですぐに解けなかった部分を解きなおしたりしていました。制限時間いっぱいまで解答に使って最終結果を確認したところ、無事合格していました。あと1、2問正解していれば成績優秀者となっていたので、合格によるうれしさもあったのですが、同時に成績優秀者になれなかった残念な気持ちもありました。とはいえ、久しぶりの資格試験で合格できたのは達成感がありました。

感想とまとめ

ここまで統計検定2級についていろいろ書いてきました。久しぶりの試験ということで試験勉強の仕方から模索する毎日でしたが、試験当日まで充実していた気がします。勉強時間は計測していなかったのではっきりとは言えませんが、数十時間くらいではないでしょうか。 100時間は超えていなかったように思えます。試験当日は想像以上に緊張してしまいましたが、たまにこのような緊張感のある試験を受けてみるというのも、メリハリをつけるためにはよいと思いました。

統計検定2級に向けて勉強を始めたあと、仕事でも役立つ場面もありました。統計学の観点から機械学習や深層学習のアルゴリズムを見直すことでアルゴリズムに対する理解が深まったり、これまでおぼろげながら理解していた正規分布などについてもはっきりと理解できました。まだまだPRMLなどの数式の多い本などは難しく感じますが、統計検定2級の勉強により用語を理解したことで、前よりは取っつきやすくなった気がします。

今後は統計検定1級の合格を目指したいと思います。統計検定には準1級もありますが、こちらは幅広く浅い知識を問われる試験であると聞き、数式を追って理論を理解するための統計学の基礎を学びたい私にとってはすこし目指しているところが違う試験と感じました。また準1級でも2級と同じCBTによる試験が開始されるかされないかの微妙な時期でもあり、試験方式が安定している1級を目指したほうがある意味やりやすいと感じたのもあります。

久しぶりの資格試験ということもあり、合格体験談を書いてみました。ここで書いた内容が統計検定2級を受験するすべての人に参考になるとは思いませんが、試験勉強の参考となれば幸いです。

2021-01-15

【機械学習】バイアスとバリアンスのトレードオフ

機械学習 Python

毎回悩むことの多いので、モデルの予測誤差を構成するバイアス（偏り）とバリアンス（分散）についてまとめる。

平均二乗誤差（MSE）

機械学習において、モデルの予測誤差を測る指標の1つとして 平均二乗誤差（MSE） がある。 MSEは、真の値を $y$ 、モデルの予測値を $\hat{y}$ として次のように表される。

$\begin{align} E \left[ \left( y - \hat{y} \right)^{2} \right] \end{align}$

バイアス-バリアンス分解

平均二乗誤差の式を変形すると、

$\begin{align} E \left[ \left( y - \hat{y} \right)^{2} \right] &= E \left[ \left( y - E \left[ \hat{y} \right] + E \left[ \hat{y} \right] - \hat{y} \right)^{2} \right] \\ &= E \left[ \left( y - E \left[ \hat{y} \right] \right)^{2} + 2 \left( y - E \left[ \hat{y} \right] \right) \left( E \left[ \hat{y} \right] - \hat{y} \right) + \left( \hat{y} - E \left[ \hat{y} \right] \right)^{2} \right] \\ &= E \left[ \left( y - E \left[ \hat{y} \right] \right)^{2} + \left( \hat{y} - E \left[ \hat{y} \right] \right)^{2} \right] \\ &= E \left[ \left( y - E \left[ \hat{y} \right] \right)^{2} \right] + E \left[ \left( \hat{y} - E \left[ \hat{y} \right] \right)^{2} \right] \end{align}$

のように2つの項に分解できる。第1項が バイアス、第2項が バリアンス であり、モデルの予測誤差をバイアスとバリアンスに分解することを バイアス-バリアンス分解 と呼ぶ。

バイアス、バリアンスの意味

バイアスとバリアンスの意味を考える。

バイアスは、

$\begin{align} E \left[ \left( y - E \left[ \hat{y} \right] \right)^{2} \right] \end{align}$

で表される。モデルの予測値 $\hat{y}$ の期待値と真の値 $y$ の差が小さいほど、バイアスが小さくなる。すなわち、データに対するモデルのあてはまりの良さを測定していると言え、バイアスが小さいほど学習に使用したデータにより適合していると言える。

バリアンスは、

$\begin{align} E \left[ \left( \hat{y} - E \left[ \hat{y} \right] \right)^{2} \right] \end{align}$

で表される。バリアンスの名前の通り、モデルの予測値に対する分散を示している。モデルの予測値 $\hat{y}$ とその期待値の差が小さいほどバリアンスが小さくなることから、バリアンスが小さいモデルは安定していると言える。

バイアス・バリアンスのトレードオフ

学習に使用するデータがノイズを含んでいる場合を想定する。

バイアスが小さくなるように（よりデータに適合するように）モデルを構築した場合、そのモデルはデータのノイズに対しても適合していることになる。このため、小さいデータの値変動（ノイズ）に対してモデルの予測結果が不安定になりがちであり、バリアンスが大きいモデルと言える。

バリアンスが小さくなるように（データの値変動に対して無頓着な）モデルを構築した場合、モデルの予測結果は安定する一方で、そのモデルはデータの特徴を十分に捉えきれていないものになる。このためモデルはデータに対して適合していないことになり、バイアスが大きくなる。

ここまでの議論により、バイアスとバリアンスの両方を同時に小さくすることはできず、互いにトレードオフの関係にあることがわかる。このことを バイアス・バリアンスのトレードオフ 呼ぶ。

バイアス・バリアンスのトレードオフを確認するプログラム

実際にバイアス・バリアンスのトレードオフを確認するため、次のようなPythonプログラムを作成した。このプログラムでは、sin曲線にノイズを加えた30個の学習データに対して1次・3次・10次・20次の多項式をfitさせ、バイアスとバリアンスがそれぞれの場合についてどのような値を取るかを確認する。

import numpy as np
import matplotlib.pyplot as plt
from math import pi

np.random.seed(0)


# Prepare data. (2*sin(x) + noise)
X_train = np.linspace(0, 1, 30)
y_train = 1.0 * np.sin(X_train * 2 * pi) + np.random.rand(*X_train.shape) - 0.5

# Predict with polynomial function.
def predict(X, y, degree):
    w = np.polyfit(X, y, degree)
    f = np.poly1d(w)
    y_pred = f(X_train)
    
    return y_pred

degrees = [1, 3, 10, 20]
y_predicts = []
for deg in degrees:
    y_predicts.append(predict(X_train, y_train, deg))

# Draw train data and predict.
fig = plt.figure(figsize=(12, 12))
fig.patch.set_alpha(1)
for i, (deg, y_pred) in enumerate(zip(degrees, y_predicts)):
    plt.subplot(2, 2, i+1)
    plt.plot(X_train, y_train, ".", X_train, y_pred, "-")
    plt.title(f"degree={deg}")
    plt.xlabel("X")
    plt.ylabel("y")

# Calculate bias and variance.
biases = []
variances = []
for i, (deg, y_pred) in enumerate(zip(degrees, y_predicts)):
    biases.append(np.mean((y_train - y_pred)**2))
    variances.append(np.mean((y_pred - np.mean(y_pred))**2))

# Draw biases and variances.
fig = plt.figure(figsize=(6, 6))
fig.patch.set_alpha(1)
bar_1 = plt.bar(np.arange(len(degrees)), biases, tick_label=degrees, width=0.3)
bar_2 = plt.bar(np.arange(len(degrees)) + 0.3, variances, tick_label=degrees, width=0.3)
plt.xlabel("degree")
plt.legend((bar_1, bar_2), ("Bias", "Variance"))

上記のプログラムを実行すると、最初に学習データと学習データに対してfitさせた多項式の図が表示される。ノイズ成分からの影響が少なく、学習データの特徴をうまく捉えることに成功しているのは3次の多項式モデルであると言える。一方で多項式の次数が10次や20次にもなると、学習データのノイズを拾うようになる。

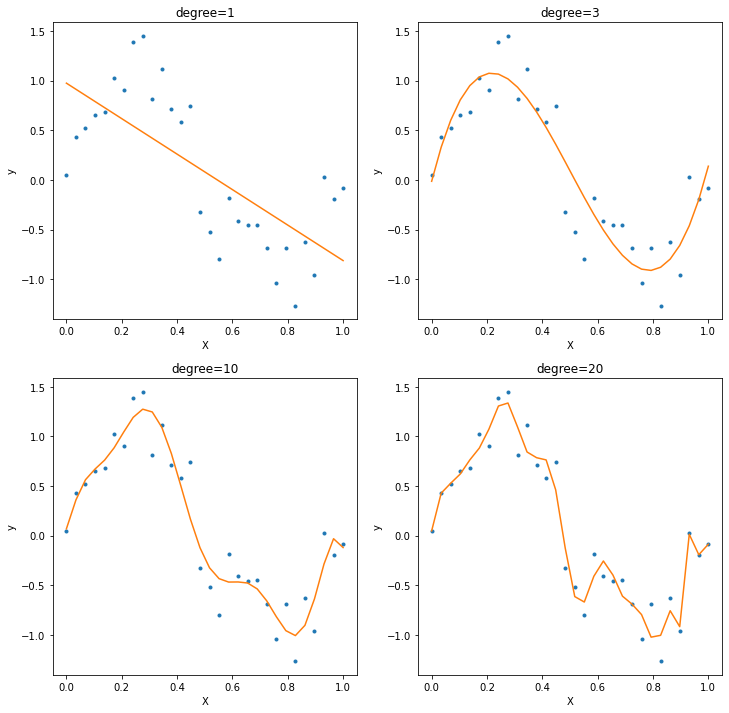
f:id:nuka137:20210120074811p:plain

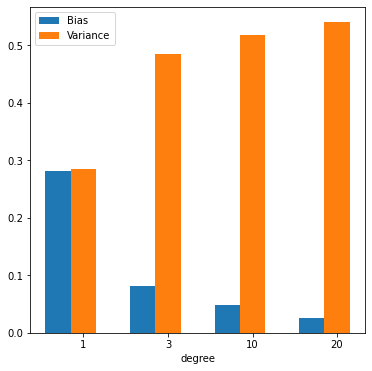
2つ目に出力される図は、各多項式の次数に対してバイアスとバリアンスの値をグラフにしたものである。次数を増やすことにより、バイアスが減少していく一方でバリアンスが増加していくことがわかる。この例からも、バイアスとバリアンスを両方同時に小さくできないこと（バイアス・バリアンスのトレードオフ）が確認できた。

f:id:nuka137:20210120075452p:plain

参考文献

はじめてのパターン認識（著者：平井有三） 2章
https://axa.biopapyrus.jp/machine-learning/model-evaluation/bias-variance-tradeoff.html
https://en.wikipedia.org/wiki/Bias%E2%80%93variance_tradeoff

2020-10-12

【統計学入門（東京大学出版会）】第13章練習問題解答

統計学

東京大学出版会から出版されている統計学入門（基礎統計学Ⅰ）について第13章の練習問題の解答を書いていく。

本章以外の解答
13.1
- i)
- ii)
- iii)
- iv)
- v)
13.2
- i)
- ii)
- iii)
- iv)

本章以外の解答

本章以外の練習問題の解答は別の記事で公開している。
必要に応じて参照されたい。

13.1

i)

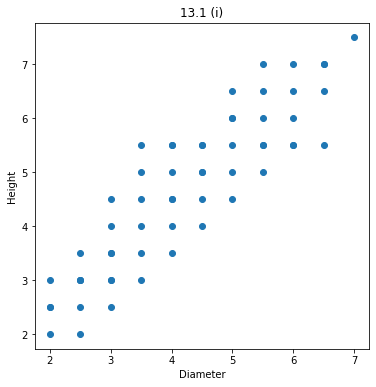
散布図を作成するPythonプログラムを次に示す。

import matplotlib.pyplot as plt

diameter = [
    2, 2, 2, 2, 2.5, 2.5, 2.5, 2.5, 2.5, 2.5, 3, 3, 3, 3, 3, 3, 3, 3.5,
    3.5, 3.5, 3.5, 3.5, 3.5, 4, 4, 4, 4, 4, 4, 4, 4.5, 4.5, 4.5, 4.5, 4.5, 4.5, 5, 5,
    5, 5, 5, 5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 6, 6, 6, 6, 6, 6.5, 6.5, 6.5, 6.5, 7,
]
height = [
    2, 2.5, 2.5, 3, 2, 2.5, 3, 3, 3, 3.5, 2.5, 3, 3, 3.5, 3.5, 4, 4.5, 3,
    3.5, 4, 4.5, 5, 5.5, 3.5, 4, 4.5, 4.5, 5, 5.5, 5.5, 4, 4.5, 5, 5, 5.5, 5.5, 6, 4.5,
    5, 5.5, 6, 6.5, 5, 5.5, 5.5, 6, 6.5, 7, 5.5, 5.5, 6, 6.5, 7, 5.5, 6.5, 7, 7, 7.5,
]

fig = plt.figure(figsize=(6, 6))
fig.patch.set_alpha(1)

plt.subplot(1, 1, 1)
plt.scatter(diameter, height)
plt.xlabel("Diameter")
plt.ylabel("Height")
plt.title("13.1 (i)")

上記のプログラムを実行すると、次の図が得られる。

f:id:nuka137:20201012072055p:plain

ii)

直径を $X_{i}$ 、その標本平均を $\bar{X}$ 、樹高を $Y_{i}$ 、その標本平均を $\bar{Y}$ とすると、標本回帰方程式、

$\begin{align} Y = \hat{\beta}_{1} + \hat{\beta}_{2} X \end{align}$

$\begin{align} \hat{\beta}_{1} = \bar{Y} - \hat{\beta}_{2} \bar{X} \end{align}$

$\begin{align} \hat{\beta}_{2} = \frac{ \sum (X_{i} - \bar{X})(Y_{i} - \bar{Y}) }{\sum (X_{i} - \bar{X})^{2}} \end{align}$

となる。

Pythonプログラム

import numpy as np

diameter = np.array([
    2, 2, 2, 2, 2.5, 2.5, 2.5, 2.5, 2.5, 2.5, 3, 3, 3, 3, 3, 3, 3, 3.5,
    3.5, 3.5, 3.5, 3.5, 3.5, 4, 4, 4, 4, 4, 4, 4, 4.5, 4.5, 4.5, 4.5, 4.5, 4.5, 5, 5,
    5, 5, 5, 5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 6, 6, 6, 6, 6, 6.5, 6.5, 6.5, 6.5, 7,
])
height = np.array([
    2, 2.5, 2.5, 3, 2, 2.5, 3, 3, 3, 3.5, 2.5, 3, 3, 3.5, 3.5, 4, 4.5, 3,
    3.5, 4, 4.5, 5, 5.5, 3.5, 4, 4.5, 4.5, 5, 5.5, 5.5, 4, 4.5, 5, 5, 5.5, 5.5, 6, 4.5,
    5, 5.5, 6, 6.5, 5, 5.5, 5.5, 6, 6.5, 7, 5.5, 5.5, 6, 6.5, 7, 5.5, 6.5, 7, 7, 7.5,
])

beta2 = np.sum((diameter - np.mean(diameter)) * (height - np.mean(height))) / np.sum((diameter - np.mean(diameter))**2)
beta1 = np.mean(height) - beta2 * np.mean(diameter)

print(f"y = {beta2} x + {beta1}")

を実行することにより、標本回帰係数 $\hat{\beta}_{1}, \hat{\beta}_{2}$ が求まり、標本回帰方程式が次のように得られる。

y = 0.9324473104749922 x + 0.7261717521233093

iii)

標本回帰方程式の傾き $\beta_{2}$ の検定を行う。帰無仮説を $\beta_{2} = 0.9$ 、対立仮説を $\beta_{2} \neq 0.9$ とする。

回帰残差 $\hat{e}_{i}$ 、標準誤差 $s.e. (\hat{\beta}_{2})$ は、

$\begin{align} \hat{e}_{i} = Y_{i} - \hat{\beta}_{1} - \hat{\beta}_{2} X_{i} \end{align}$

$\begin{align} s.e. ( \hat{\beta}_{2} ) = \frac{ \sqrt{ \sum \hat{e}_{i}^{2} / (n-2) } }{ \sqrt{ \sum (X_{i} - \hat{X})^{2} } } \end{align}$

で与えられ、

$\begin{align} t = \frac{\hat{\beta}_{2} - \beta_{2}}{s.e. (\hat{\beta_{2}})} \end{align}$

は自由度 $n-2$ のスチューデントのt分布に従う。

このため、

$\begin{align} -t_{0.025} \le t \le t_{0.025} \end{align}$

が成り立つとき、直径が1寸延びれば0.9尺だけ高くなる仮説が有意水準5%で棄却されない。

このことについてPythonプログラムを使って調べる。

import numpy as np
from scipy.stats import t

diameter = np.array([
    2, 2, 2, 2, 2.5, 2.5, 2.5, 2.5, 2.5, 2.5, 3, 3, 3, 3, 3, 3, 3, 3.5,
    3.5, 3.5, 3.5, 3.5, 3.5, 4, 4, 4, 4, 4, 4, 4, 4.5, 4.5, 4.5, 4.5, 4.5, 4.5, 5, 5,
    5, 5, 5, 5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 6, 6, 6, 6, 6, 6.5, 6.5, 6.5, 6.5, 7,
])
height = np.array([
    2, 2.5, 2.5, 3, 2, 2.5, 3, 3, 3, 3.5, 2.5, 3, 3, 3.5, 3.5, 4, 4.5, 3,
    3.5, 4, 4.5, 5, 5.5, 3.5, 4, 4.5, 4.5, 5, 5.5, 5.5, 4, 4.5, 5, 5, 5.5, 5.5, 6, 4.5,
    5, 5.5, 6, 6.5, 5, 5.5, 5.5, 6, 6.5, 7, 5.5, 5.5, 6, 6.5, 7, 5.5, 6.5, 7, 7, 7.5,
])

beta2 = 0.9324473104749922
beta1 = 0.7261717521233093
pred = beta1 + beta2 * diameter
e = height - pred
n = height.size

s = np.sum(e**2) / (n - 2)
se = np.sqrt(s)
beta2_se = se / np.sqrt(np.sum((diameter - np.mean(diameter))**2))

criteria = (beta2 - 0.9) / beta2_se
rejection = t.ppf(q=1-0.025, df=n-2)

print("Rejection: |t| > |{}|, Criteria: {}, {}".format(rejection, criteria, "Accept" if abs(criteria) < abs(rejection) else "Reject"))

上記のプログラムを実行すると、

Rejection: |t| > |2.0032407174966975|, Criteria: 0.5132092804206397, Accept

が得られ、直径が1寸延びれば0.9尺だけ高くなると言える。

iv)

iii)において、

$\begin{align} abs(\hat{e}_{i}^{2}) \gt 2 \cdot s.e. ( \hat{\beta}_{2} ) \end{align}$

を満たす標本が存在するか否かを確認する。

Pythonプログラム

import numpy as np
from scipy.stats import t

diameter = np.array([
    2, 2, 2, 2, 2.5, 2.5, 2.5, 2.5, 2.5, 2.5, 3, 3, 3, 3, 3, 3, 3, 3.5,
    3.5, 3.5, 3.5, 3.5, 3.5, 4, 4, 4, 4, 4, 4, 4, 4.5, 4.5, 4.5, 4.5, 4.5, 4.5, 5, 5,
    5, 5, 5, 5, 5.5, 5.5, 5.5, 5.5, 5.5, 5.5, 6, 6, 6, 6, 6, 6.5, 6.5, 6.5, 6.5, 7,
])
height = np.array([
    2, 2.5, 2.5, 3, 2, 2.5, 3, 3, 3, 3.5, 2.5, 3, 3, 3.5, 3.5, 4, 4.5, 3,
    3.5, 4, 4.5, 5, 5.5, 3.5, 4, 4.5, 4.5, 5, 5.5, 5.5, 4, 4.5, 5, 5, 5.5, 5.5, 6, 4.5,
    5, 5.5, 6, 6.5, 5, 5.5, 5.5, 6, 6.5, 7, 5.5, 5.5, 6, 6.5, 7, 5.5, 6.5, 7, 7, 7.5,
])

beta2 = 0.9324473104749922
beta1 = 0.7261717521233093
pred = beta1 + beta2 * diameter
e = height - pred
n = height.size

s = np.sum(e**2) / (n - 2)
se = np.sqrt(s)

over_2se = np.abs(e) > 2 * se
if over_2se.sum() > 0:
    print("Exist")
    over_diameter = diameter[over_2se]
    over_height = height[over_2se]
    for d, h in zip(over_diameter, over_height):
        print("({}, {})".format(d, h))
else:
    print("Not exist")

より、

Exist
(3.5, 5.5)

が得られ、(直径, 樹高) = (3.5, 5.5) の標本が標本回帰直線から2s.e.以上外れた樹木であるとわかる。

v)

ii)で得られた結果を使い、直径8寸のときの樹高を推定すればよい。

y = 0.9324473104749922 x + 0.7261717521233093

Pythonプログラム

beta2 = 0.9324473104749922
beta1 = 0.7261717521233093
pred = beta1 + beta2 * 8

print(pred)

により、

8.185750235923248

が得られる。

13.2

i)

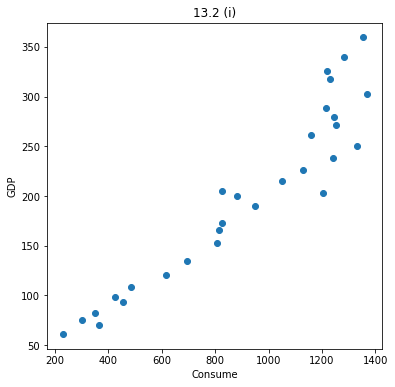
散布図を作成するPythonプログラムを次に示す。

import numpy as np
import matplotlib.pyplot as plt

consume = np.array([
    229, 367, 301, 352, 457, 427, 485, 616,
    695, 806, 815, 826, 951, 1202, 881, 827, 1050, 1127, 1241,
    1330, 1158, 1254, 1243, 1216, 1368, 1231, 1219, 1284, 1355,
])
gdp = np.array([
    61.2, 70.0, 74.9, 82.8, 93.6, 98.5, 108.8, 120.1,
    135.1, 152.5, 165.8, 173.0, 189.9, 202.6, 199.7, 205.0, 214.9, 226.3, 238.1,
    250.7, 261.4, 271.0, 279.3, 288.4, 303.0, 317.3, 325.7, 340.3, 359.5,
])

fig = plt.figure(figsize=(6, 6))
fig.patch.set_alpha(1)

plt.subplot(1, 1, 1)
plt.scatter(consume, gdp)
plt.xlabel("Consume")
plt.ylabel("GDP")
plt.title("13.2 (i)")

上記プログラムを実行すると、次の図が得られる。

f:id:nuka137:20201012082849p:plain

ii)

実質GDPを $X_{i}$ 、銅消費量を $Y_{i}$ としたとき、標本回帰方程式、

$\begin{align} \log Y = \hat{\beta}_{1} + \hat{\beta}_{2} \log X \end{align}$

$\begin{align} \hat{\beta}_{1} = mean(\log Y) - \hat{\beta}_{2} \cdot mean(\log X) \end{align}$

$\begin{align} \hat{\beta}_{2} = \frac{ \sum (\log X_{i} - mean(\log X) )(\log Y_{i} - mean(\log Y) ) }{\sum (\log X_{i} - mean (\log X) )^{2}} \end{align}$

となる。

Pythonプログラム

import numpy as np

gdp = np.array([
    61.2, 70.0, 74.9, 82.8, 93.6, 98.5, 108.8, 120.1,
    135.1, 152.5, 165.8, 173.0, 189.9, 202.6, 199.7, 205.0, 214.9, 226.3, 238.1,
    250.7, 261.4, 271.0, 279.3, 288.4, 303.0, 317.3, 325.7, 340.3, 359.5,
])
consume = np.array([
    229, 367, 301, 352, 457, 427, 485, 616,
    695, 806, 815, 826, 951, 1202, 881, 827, 1050, 1127, 1241,
    1330, 1158, 1254, 1243, 1216, 1368, 1231, 1219, 1284, 1355,
])

consume_log = np.log(consume)
gdp_log = np.log(gdp)

beta2 = np.sum((gdp_log - np.mean(gdp_log)) * (consume_log - np.mean(consume_log))) / np.sum((gdp_log - np.mean(gdp_log))**2)
beta1 = np.mean(consume_log) - beta2 * np.mean(gdp_log)

print(f"log(y) = {beta2} log(x) + {beta1}")

を実行することにより、標本回帰係数 $\hat{\beta}_{1}, \hat{\beta}_{2}$ が求まり、標本回帰方程式が次のように得られる。

log(y) = 0.966869094731703 log(x) + 1.6898916241200759

iii)

実質GDPが4%/年で増加すると仮定すると、2000年の銅消費量 $Y_{2020}$ は、

$\begin{align} Y_{2000} = Y_{1988} \cdot (1 + 0.04 \hat{\beta}_{2}) \cdot (2000 - 1988) \end{align}$

であるから、ii)の結果を利用してPythonプログラム

consume_1988 = 1355
beta_2 = 0.966869094731703
pred = consume_1988 * (1 + beta_2 * 0.04)**(2000-1988)
print(pred)

により、2000年の銅消費量、

2136.457480272669

が得られる。

iv)

標本回帰方程式の傾き $\beta_{2}$ の検定を行う。帰無仮説を $\beta_{2} = 1$ 、対立仮説を $\beta_{2} \neq 1$ とする。

回帰残差 $\hat{e}_{i}$ 、標準誤差 $s.e. (\hat{\beta}_{2})$ は、

$\begin{align} \hat{e}_{i} = \log Y_{i} - \hat{\beta}_{1} - \hat{\beta}_{2} \log X_{i} \end{align}$

$\begin{align} s.e. ( \hat{\beta}_{2} ) = \frac{ \sqrt{ \sum \hat{e}_{i}^{2} / (n-2) } }{ \sqrt{ \sum (\log X_{i} - mean(\log X) )^{2} } } \end{align}$

で与えられ、

$\begin{align} t = \frac{\hat{\beta}_{2} - \beta_{2}}{s.e. (\hat{\beta}_{2})} \end{align}$

は自由度 $n-2$ のスチューデントのt分布に従う。

このため、

$\begin{align} -t_{0.025} \le t \le t_{0.025} \end{align}$

が成り立つとき、銅消費量のGDP弾性値が1であるという仮説が有意水準5%で棄却されない。

このことについてPythonプログラムを使って調べる。

import numpy as np
from scipy.stats import t

gdp = np.array([
    61.2, 70.0, 74.9, 82.8, 93.6, 98.5, 108.8, 120.1,
    135.1, 152.5, 165.8, 173.0, 189.9, 202.6, 199.7, 205.0, 214.9, 226.3, 238.1,
    250.7, 261.4, 271.0, 279.3, 288.4, 303.0, 317.3, 325.7, 340.3, 359.5,
])
consume = np.array([
    229, 367, 301, 352, 457, 427, 485, 616,
    695, 806, 815, 826, 951, 1202, 881, 827, 1050, 1127, 1241,
    1330, 1158, 1254, 1243, 1216, 1368, 1231, 1219, 1284, 1355,
])

consume_log = np.log(consume)
gdp_log = np.log(gdp)


beta2 = 0.966869094731703
beta1 = 1.6898916241200759
pred = beta1 + beta2 * gdp_log
e = consume_log - pred
n = consume_log.size

s = np.sum(e**2) / (n - 2)
se = np.sqrt(s)
beta2_se = se / np.sqrt(np.sum((gdp_log - np.mean(gdp_log))**2))

criteria = (beta2 - 1) / beta2_se
rejection = t.ppf(q=1-0.025, df=n-2)

print("Rejection: |t| > |{}|, Criteria: {}, {}".format(rejection, criteria, "Accept" if abs(criteria) < abs(rejection) else "Reject"))

上記を実行すると、

Rejection: |t| > |2.0518305164802833|, Criteria: -0.7251395116305018, Accept

が得られ、銅消費量のGDP弾性値が1であるといえる。

2020-10-11

【統計学入門（東京大学出版会）】第12章練習問題解答

統計学

東京大学出版会から出版されている統計学入門（基礎統計学Ⅰ）について第12章の練習問題の解答を書いていく。

本章以外の解答
12.1
12.2
- i)
- ii)
- iii)
12.3
12.4
12.5
- i)
- ii)
12.6
12.7
12.8
- i)
- ii)
12.9
12.10

本章以外の解答

本章以外の練習問題の解答は別の記事で公開している。
必要に応じて参照されたい。

12.1

標本平均を $\bar{X}$ 、母平均を $\mu$ 、標本分散を $s^{2}$ 、標本数を $n$ とすると、

$\begin{align} t = \frac{\bar{X} - \mu}{\sqrt{s^{2} / n}} \end{align}$

は、自由度 $n$ のスチューデントのt分布に従うことを利用する。

帰無仮説を $\mu = 100$ 、対立仮説を $\mu \neq 100$ とすると、

$\begin{align} -t_{0.025} \lt t \lt t_{0.025} \end{align}$

を満たすときに、有意水準5%で母平均が100gと考えてよいと判断できる。

これをPythonのプログラムによって確認する。

import numpy as np
from math import sqrt
from scipy.stats import t

x = np.array([101.1, 103.2, 102.1, 99.2, 100.5, 101.3, 99.7, 100.5, 98.9, 101.4])
n = x.size
x_bar = x.mean()
s2 = np.sum((x - x_bar)**2) / (n - 1)
mu = 100

criteria = (x_bar - mu) / sqrt(s2 / n)
rejection = t.ppf(q=1-0.025, df=n-1)

print("Rejection: t < {} or {} < t, Criteria: {}, {}".format(-rejection, rejection, criteria, "Rejected" if abs(criteria) > rejection else "Accepted"))

上記のプログラムを実行すると、

Rejection: t < -2.2621571627409915 or 2.2621571627409915 < t, Criteria: 1.8909240092503048, Accepted

が得られ、母平均100gは有意水準5%で棄却されない。

12.2

i)

標本間の母分散が同じであるから、2標本の標本分散を $s^{2}$ とすると、

$\begin{align} t = \frac{(\bar{X} - \bar{Y}) - (\mu_{X} - \mu_{Y}) }{s\sqrt{1/m + 1/n}} \end{align}$

は、自由度が $m + n - 1$ のスチューデントのt分布に従う。

なお、男の給与の標本平均を $\bar{X}$ 、標本数を $m$ 、母平均を $\mu_{X}$ とし、女の給与の標本平均を $\bar{Y}$ 、標本数を $n$ 、母平均を $\mu_{Y}$ とする。なお標本間の母分散が同じであるから、2標本の標本分散 $s^{2}$ は、

$\begin{align} s^{2} = \frac{1}{m+n-2} \left( \sum_{i=1}^{n} ( X_{i} - \bar{X} )^{2} + \sum_{i=1}^{m} ( Y_{i} - \bar{Y} )^{2} \right) \end{align}$

となる。

帰無仮説を $\mu_{X} = \mu_{Y}$ 、対立仮説を $\mu_{X} \neq \mu_{Y}$ とすると、

$\begin{align} -t_{0.025} \lt t \lt t_{0.025} \end{align}$

を満たすときに、有意水準5%で男女の賃金格差が存在しないと考えてよいと判断できる。

これをPythonのプログラムによって確認する。

import numpy as np
from math import sqrt
from scipy.stats import t

x = np.array([15.4, 18.3, 16.5, 17.4, 18.9, 17.2, 15.0, 15.7, 17.9, 16.5])
y = np.array([14.2, 15.9, 16.0, 14.0, 17.0, 13.8, 15.2, 14.5, 15.0, 14.4])
m = x.size
n = y.size
x_bar = x.mean()
y_bar = y.mean()
s = sqrt((np.sum((x - x_bar)**2) + np.sum((y - y_bar)**2)) / (m + n - 2))

criteria = (x_bar - y_bar) / (s * sqrt(1 / m + 1 / n))
rejection = t.ppf(q=1-0.025, df=m+n-2)

print("Rejection: t < {} or {} < t, Criteria: {}, {}".format(-rejection, rejection, criteria, "Rejected" if abs(criteria) > rejection else "Accepted"))

上記のプログラムを実行すると、

Rejection: t < -2.10092204024096 or 2.10092204024096 < t, Criteria: 3.606503775109937, Rejected

が得られ、男女の賃金格差が存在しないことは有意水準5%で棄却される。すなわち、男女の賃金格差が存在する。

ii)

男の給与の標本平均を $\bar{X}$ 、標本分散を $s_{X}^{2}$ 、標本数を $m$ 、母平均を $\mu_{X}$ とし、女の給与の標本平均を $\bar{Y}$ 、標本分散を $s_{Y}^{2}$ 、標本数を $n$ 、母平均を $\mu_{Y}$ とする。

標本間の分散が等しくない場合、

$\begin{align} t = \frac{(\bar{X} - \bar{Y}) - (\mu_{X} - \mu_{Y}) }{\sqrt{s_{X}^{2}/m + s_{Y}^{2}/n}} \end{align}$

は、スチューデントのt分布に従う（ウェルチの検定）。

なお自由度 $\nu$ は、

$\begin{align} \nu = \frac{(s_{X}^{2} / m + s_{Y}^{2} / n)^{2}}{\frac{(s_{X}^{2}/m)^{2}}{m-1} + \frac{(s_{Y}^{2}/n)^{2}}{n-1}} \end{align}$

となる。

帰無仮説を $\mu_{X} = \mu_{Y}$ 、対立仮説を $\mu_{X} \neq \mu_{Y}$ とすると、

$\begin{align} -t_{0.025} \lt t \lt t_{0.025} \end{align}$

を満たすときに、有意水準5%で男女の賃金格差が存在しないと考えてよいと判断できる。

これをPythonのプログラムによって確認する。

import numpy as np
from math import sqrt
from scipy.stats import t
from decimal import Decimal, ROUND_HALF_UP

x = np.array([15.4, 18.3, 16.5, 17.4, 18.9, 17.2, 15.0, 15.7, 17.9, 16.5])
y = np.array([14.2, 15.9, 16.0, 14.0, 17.0, 13.8, 15.2, 14.5, 15.0, 14.4])
m = x.size
n = y.size
x_bar = x.mean()
y_bar = y.mean()
s12 = (np.sum((x - x_bar)**2)) / (m - 1)
s22 = (np.sum((y - y_bar)**2)) / (n - 1)
nu = (s12 / m + s22 / n)**2 / ((s12 / m)**2 / (m-1) + (s22 / n)**2 / (n-1))
nu = int(Decimal(str(nu)).quantize(Decimal('0'), rounding=ROUND_HALF_UP))

criteria = (x_bar - y_bar) / sqrt(s12 / m + s22 / n)
rejection = t.ppf(q=1-0.025, df=nu)

print(f"nu: {nu}")
print("Rejection: t < {} or {} < t, Criteria: {}, {}".format(-rejection, rejection, criteria, "Rejected" if abs(criteria) > rejection else "Accepted"))

上記のプログラムを実行すると、

nu: 17
Rejection: t < -2.1098155778331806 or 2.1098155778331806 < t, Criteria: 3.606503775109937, Rejected

が得られ、男女の賃金格差が存在しないことは有意水準5%で棄却される。すなわち、男女の賃金格差が存在する。

iii)

男の給与の標本分散を $s_{X}^{2}$ 、標本数を $m$ 、母分散を $\sigma_{X}^{2}$ とし、女の給与の標本分散を $s_{Y}^{2}$ 、標本数を $n$ 、母分散を $\sigma_{Y}^{2}$ とする。

このとき、

$\begin{align} F = \frac{s_{1}^{2}}{s_{2}^{2}} \end{align}$

は、自由度が $(m-1, n-1)$ のF分布に従う。

帰無仮説を $\sigma_{X}^{2} = \sigma_{Y}^{2}$ 、対立仮説を $\sigma_{X}^{2} \neq \sigma_{Y}^{2}$ とすると、

$\begin{align} F \lt F_{0.005} \end{align}$

を満たすときに、有意水準1%で男女の賃金の母分散が等しいと判断できる。

これをPythonのプログラムによって確認する。

import numpy as np
from scipy.stats import f

x = np.array([15.4, 18.3, 16.5, 17.4, 18.9, 17.2, 15.0, 15.7, 17.9, 16.5])
y = np.array([14.2, 15.9, 16.0, 14.0, 17.0, 13.8, 15.2, 14.5, 15.0, 14.4])
m = x.size
n = y.size
s12 = (np.sum((x - x_bar)**2)) / (m - 1)
s22 = (np.sum((y - y_bar)**2)) / (n - 1)

criteria = s12 / s22
rejection = f.ppf(q=1-0.005, dfn=m-1, dfd=n-1)

print("Rejection: F > {}, Criteria: {}, {}".format(rejection, criteria, "Rejected" if criteria > rejection else "Accepted"))

上記のプログラムを実行すると、

Rejection: F > 6.541089626853058, Criteria: 1.5635220125786158, Accepted

が得られ、男女の賃金の母分散が等しいことは有意水準1%で棄却されない。

12.3

治療法が有効か否かを判断するためには、治療後に血圧測定値が下がっていることを確認すればよい。したがって、治療前後の血圧測定値の差の平均を $\mu$ としたときに、帰無仮定 $\mu = 0$ 、対立仮定 $\mu \lt 0$ として検定する。

このために、

$\begin{align} t = \frac{\bar{X} - \mu}{\sqrt{s^{2} / n}} \end{align}$

が自由度 $n - 1$ のスチューデントのt分布に従うことを利用する。ここで、標本平均を $\bar{X}$ 、標本分散を $s^{2}$ 、標本数を $n$ とした。

$\begin{align} t \le -t_{0.01} \end{align}$

を満たすときに帰無仮定が棄却され、有意水準1%で治療前後の血圧測定値の差があり、治療の効果があると判断できる。

これをPythonのプログラムによって確認する。

import numpy as np
from math import sqrt
from scipy.stats import t

x = np.array([2, -5, -4, -8, 3, 0, 3, -6, -2, 1, 0, -4])
n = x.size
x_bar = x.mean()
s2 = np.sum((x - x_bar)**2) / (n - 1)
mu = 0

criteria = (x_bar - mu) / sqrt(s2 / n)
rejection = t.ppf(q=1-0.01, df=n-1)

print("Rejection: t < {}, Criteria: {}, {}".format(-rejection, criteria, "Rejected" if criteria < -rejection else "Accepted"))

上記のプログラムを実行すると、

Rejection: t < -2.7180791835355564, Criteria: -1.560009076442849, Accepted

が得られ、帰無仮定は棄却されない。このため、有意水準1%で治療前後の血圧測定値の差がないと判断でき、治療の効果がないと言える。

12.4

仮定された理論上での確率分布の適合度の検定であるから、適合度の $\chi^{2}$ 検定を用いる。すなわち、観測度数を $f_{i}$ 、理論確率を $p_{i} = \frac{1}{6}$ とする。

なお表より $f_{i}$ は、

数字	$f_{i}$
1	10
2	7
3	8
4	11
5	6
6	8

である。

$\begin{align} \chi^{2} = \sum_{i=1}^{k} \frac{( f_{i} - n p_{i} )^{2}}{n p_{i}} \end{align}$

が自由度 $n - 1$ の $\chi^{2}$ 分布に従うことを利用すると、

$\begin{align} \chi^{2} \gt \chi_{0.05}^{2} \end{align}$

を満たすときに、有意水準5%でさいころが正しく作られていないと判断できる。

これをPythonのプログラムによって確認する。

import numpy as np
from scipy.stats import chi2

f = np.array([10, 7, 8, 11, 6, 8])
n = np.sum(f)
p = 1 / 6

criteria = np.sum((f - n * p) ** 2 / (n * p))
rejection = chi2.ppf(q=1-0.05, df=f.size-1)

print("Rejection: chi2 > {}, Criteria: {}, {}".format(rejection, criteria, "Rejected" if criteria > rejection else "Accepted"))

上記のプログラムを実行すると、

Rejection: chi2 > 11.070497693516351, Criteria: 2.0800000000000005, Accepted

が得られ、有意水準5%でさいころが正しく作られていると言える。

12.5

i)

$\begin{align} \chi^{2} = \sum_{i=1}^{k} \frac{( f_{i} - n p_{i} )^{2}}{n p_{i}} \end{align}$

が自由度 $n - 1$ の $\chi^{2}$ 分布に従うことを利用すると、

$\begin{align} \chi^{2} \gt \chi_{0.05}^{2} \end{align}$

を満たすときに、有意水準5%で0～9の値が等確率で出現するという仮説は棄却される。

これをPythonのプログラムによって確認する。

import numpy as np
from scipy.stats import chi2
import random

random.seed(1)

idx = random.randint(0, 1000 - 100)

pi_str = """
3.
1415926535 8979323846 2643383279 5028841971 6939937510
5820974944 5923078164 0628620899 8628034825 3421170679
8214808651 3282306647 0938446095 5058223172 5359408128
4811174502 8410270193 8521105559 6446229489 5493038196
4428810975 6659334461 2847564823 3786783165 2712019091
4564856692 3460348610 4543266482 1339360726 0249141273
7245870066 0631558817 4881520920 9628292540 9171536436
7892590360 0113305305 4882046652 1384146951 9415116094
3305727036 5759591953 0921861173 8193261179 3105118548
0744623799 6274956735 1885752724 8912279381 8301194912
9833673362 4406566430 8602139494 6395224737 1907021798
6094370277 0539217176 2931767523 8467481846 7669405132
0005681271 4526356082 7785771342 7577896091 7363717872
1468440901 2249534301 4654958537 1050792279 6892589235
4201995611 2129021960 8640344181 5981362977 4771309960
5187072113 4999999837 2978049951 0597317328 1609631859
5024459455 3469083026 4252230825 3344685035 2619311881
7101000313 7838752886 5875332083 8142061717 7669147303
5982534904 2875546873 1159562863 8823537875 9375195778
1857780532 1712268066 1300192787 6611195909 2164201989
"""
pi_str = pi_str.replace(" ", "").replace("\n", "").replace(".", "")[idx:idx+100]

napier_str = """
2.
7182818284 5904523536 0287471352 6624977572 4709369995
9574966967 6277240766 3035354759 4571382178 5251664274
2746639193 2003059921 8174135966 2904357290 0334295260
5956307381 3232862794 3490763233 8298807531 9525101901
1573834187 9307021540 8914993488 4167509244 7614606680
8226480016 8477411853 7423454424 3710753907 7744992069
5517027618 3860626133 1384583000 7520449338 2656029760
6737113200 7093287091 2744374704 7230696977 2093101416
9283681902 5515108657 4637721112 5238978442 5056953696
7707854499 6996794686 4454905987 9316368892 3009879312
7736178215 4249992295 7635148220 8269895193 6680331825
2886939849 6465105820 9392398294 8879332036 2509443117
3012381970 6841614039 7019837679 3206832823 7646480429
5311802328 7825098194 5581530175 6717361332 0698112509
9618188159 3041690351 5988885193 4580727386 6738589422
8792284998 9208680582 5749279610 4841984443 6346324496
8487560233 6248270419 7862320900 2160990235 3043699418
4914631409 3431738143 6405462531 5209618369 0888707016
7683964243 7814059271 4563549061 3031072085 1038375051
0115747704 1718986106 8739696552 1267154688 9570350354
"""
napier_str = napier_str.replace(" ", "").replace("\n", "").replace(".", "")[idx:idx+100]

pi_f = []
for i in range(10):
    pi_f.append(pi_str.count(str(i)))
pi_f = np.array(pi_f)

napier_f = []
for i in range(10):
    napier_f.append(napier_str.count(str(i)))
napier_f = np.array(napier_f)

n = 100
p = 1 / 10

rejection = chi2.ppf(q=1-0.05, df=10-1)
pi_criteria = np.sum((pi_f - n * p)**2 / (n * p))
napier_criteria = np.sum((napier_f - n * p)**2 / (n * p))

print("Rejection: chi2 > {}".format(rejection))
print("pi: {}, {}".format(pi_criteria, "Reject" if pi_criteria > rejection else "Accept"))
print("napier: {}, {}".format(napier_criteria, "Reject" if napier_criteria > rejection else "Accept"))

上記のプログラムを実行すると、

Rejection: chi2 > 16.918977604620448
pi: 5.4, Accept
napier: 6.4, Accept

が得られ、有意水準5%で0～9の値が等確率で出現するという仮説は棄却されない。すなわち、円周率 $\pi$ 、自然数の底 $e$ の小数点以下1000桁から選んだ100桁は0から9の値が等確率で出現していると言える。

ii)

桁数を1001とすることを除いて、i)と同様のことを行う。

import numpy as np
from scipy.stats import chi2

pi_str = """
3.
1415926535 8979323846 2643383279 5028841971 6939937510
5820974944 5923078164 0628620899 8628034825 3421170679
8214808651 3282306647 0938446095 5058223172 5359408128
4811174502 8410270193 8521105559 6446229489 5493038196
4428810975 6659334461 2847564823 3786783165 2712019091
4564856692 3460348610 4543266482 1339360726 0249141273
7245870066 0631558817 4881520920 9628292540 9171536436
7892590360 0113305305 4882046652 1384146951 9415116094
3305727036 5759591953 0921861173 8193261179 3105118548
0744623799 6274956735 1885752724 8912279381 8301194912
9833673362 4406566430 8602139494 6395224737 1907021798
6094370277 0539217176 2931767523 8467481846 7669405132
0005681271 4526356082 7785771342 7577896091 7363717872
1468440901 2249534301 4654958537 1050792279 6892589235
4201995611 2129021960 8640344181 5981362977 4771309960
5187072113 4999999837 2978049951 0597317328 1609631859
5024459455 3469083026 4252230825 3344685035 2619311881
7101000313 7838752886 5875332083 8142061717 7669147303
5982534904 2875546873 1159562863 8823537875 9375195778
1857780532 1712268066 1300192787 6611195909 2164201989
"""
pi_str = pi_str.replace(" ", "").replace("\n", "").replace(".", "")

napier_str = """
2.
7182818284 5904523536 0287471352 6624977572 4709369995
9574966967 6277240766 3035354759 4571382178 5251664274
2746639193 2003059921 8174135966 2904357290 0334295260
5956307381 3232862794 3490763233 8298807531 9525101901
1573834187 9307021540 8914993488 4167509244 7614606680
8226480016 8477411853 7423454424 3710753907 7744992069
5517027618 3860626133 1384583000 7520449338 2656029760
6737113200 7093287091 2744374704 7230696977 2093101416
9283681902 5515108657 4637721112 5238978442 5056953696
7707854499 6996794686 4454905987 9316368892 3009879312
7736178215 4249992295 7635148220 8269895193 6680331825
2886939849 6465105820 9392398294 8879332036 2509443117
3012381970 6841614039 7019837679 3206832823 7646480429
5311802328 7825098194 5581530175 6717361332 0698112509
9618188159 3041690351 5988885193 4580727386 6738589422
8792284998 9208680582 5749279610 4841984443 6346324496
8487560233 6248270419 7862320900 2160990235 3043699418
4914631409 3431738143 6405462531 5209618369 0888707016
7683964243 7814059271 4563549061 3031072085 1038375051
0115747704 1718986106 8739696552 1267154688 9570350354
"""
napier_str = napier_str.replace(" ", "").replace("\n", "").replace(".", "")

pi_f = []
for i in range(10):
    pi_f.append(pi_str.count(str(i)))
pi_f = np.array(pi_f)

napier_f = []
for i in range(10):
    napier_f.append(napier_str.count(str(i)))
napier_f = np.array(napier_f)

n = 1001
p = 1 / 10

rejection = chi2.ppf(q=1-0.05, df=9)
pi_criteria = np.sum((pi_f - n * p)**2 / (n * p))
napier_criteria = np.sum((napier_f - n * p)**2 / (n * p))

print("Rejection: chi2 > {}".format(rejection))
print("pi: {}, {}".format(pi_criteria, "Reject" if pi_criteria > rejection else "Accept"))
print("napier: {}, {}".format(napier_criteria, "Reject" if napier_criteria > rejection else "Accept"))

上記プログラムを実行すると、

Rejection: chi2 > 16.918977604620448
pi: 4.7842157842157835, Accept
napier: 4.804195804195803, Accept

が得られ、有意水準5%で0～9の値が等確率で出現するという仮説は棄却されない。すなわち、円周率 $\pi$ 、自然数の底 $e$ の最初から1001桁は0から9の値が等確率で出現していると言える。

12.6

喫煙習慣の有無と死亡率の独立性を検定するため、 $\chi^{2}$ 検定を行う。喫煙習慣の度数を $f_{i}$ とし、死亡率の度数を $f_{j}$ とすると、

$\begin{align} \chi^{2} = \sum_{i} \sum_{j} \frac{ ( n f_{ij} - f_{i} f_{j} )^{2} }{n f_{i} f_{j} } \end{align}$

となるが、この $\chi^{2}$ に対して、

$\begin{align} \chi^{2} \gt \chi_{0.05}^{2} \end{align}$

のとき $f_{i}$ と $f_{j}$ は関連していることになり、独立でなくなる。なお、自由度は $2 - 1 = 1$ である。

この判定をPythonのプログラムによって行う。

import numpy as np
from scipy.stats import chi2

f = np.array([[950, 117], [348, 54]])
n = np.sum(f)
criteria = 0
for i in range(len(f)):
    for j in range(len(f[0])):
        fij = f[i, j]
        fi = np.sum(f, axis=1)[i]
        fj = np.sum(f, axis=0)[j]
        criteria += (n * fij - fi * fj)**2 / (n * fi * fj)

rejection = chi2.ppf(q=1-0.05, df=1)

print("Rejection: chi2 > {}, Criteria: {}, {}".format(rejection, criteria, "Related" if criteria > rejection else "Not related"))

上記のプログラムを実行すると、

Rejection: chi2 > 3.841458820694124, Criteria: 1.728463379862236, Not related

が得られ、有意水準5%で $f_{i}$ と $f_{j}$ が関連していない（独立である）ことがわかる。したがって、喫煙習慣と死亡率には関連がないと言える。

12.7

12.6と同様である。

肥沃度の有無と所有関係が独立か否かを検定するため、 $\chi^{2}$ 検定を行う。所有関係の度数を $f_{i}$ とし、肥沃度の度数を $f_{j}$ とすると、

$\begin{align} \chi^{2} = \sum_{i} \sum_{j} \frac{ ( n f_{ij} - f_{i} f_{j} )^{2} }{n f_{i} f_{j} } \end{align}$

となるが、この $\chi^{2}$ に対して、

$\begin{align} \chi^{2} \gt \chi_{0.05}^{2} \end{align}$

のとき $f_{i}$ と $f_{j}$ は関連していることになり、独立でなくなる。なお、自由度は $(3 - 1) \times (3 - 1) = 4$ である。

この判定をPythonのプログラムによって行う。

import numpy as np
from scipy.stats import chi2

f = np.array([[36, 31, 58], [67, 60, 87], [49, 49, 80]])
n = np.sum(f)
criteria = 0
for i in range(len(f)):
    for j in range(len(f[0])):
        fij = f[i, j]
        fi = np.sum(f, axis=1)[i]
        fj = np.sum(f, axis=0)[j]
        criteria += (n * fij - fi * fj)**2 / (n * fi * fj)

rejection = chi2.ppf(q=1-0.05, df=4)

print("Rejection: chi2 > {}, Criteria: {}, {}".format(rejection, criteria, "Related" if criteria > rejection else "Not related"))

上記のプログラムを実行すると、

Rejection: chi2 > 9.487729036781154, Criteria: 1.5431365561546417, Not related

が得られ、有意水準5%で $f_{i}$ と $f_{j}$ が関連していない（独立である）ことがわかる。したがって、肥沃度の有無と所有関係には関連がないと言える。

12.8

i)

Aの度数を $f_{i}$ とし、Bの度数を $f_{j}$ とすると、独立性の $\chi^{2}$ 検定の基準は、

$\begin{align} \chi^{2} = \sum_{i} \sum_{j} \frac{ ( n f_{ij} - f_{i} f_{j} )^{2} }{n f_{i} f_{j} } \end{align}$

で表すことができる。

したがって、

$\begin{align} A = (x + z)(x + y)(y + u)(z + u) \end{align}$

とすると、

$\begin{align} \chi^{2} &= \frac{1}{nA} ( (y+u)(z+u)(xu - zy)^{2} + (x+z)(z+u)(zy-ux)^{2} + (x+y)(y+u)(yz-xu)^{2} + (x+z)(x+y)(xu-yz)^{2} ) \\ &= \frac{1}{nA} (xu - zy)^{2} ( (y+u)(x+y+z+u) + (x+z)(x+y+z+u) ) \\ &= \frac{1}{nA} (xu - zy)^{2} n^{2} (xu - zy)^{2} \\ &= \frac{n}{A} (xu - zy)^{2} \\ &= \frac{n (xu - zy)^{2}}{(x+z)(y+u)(x+y)(z+u)} \end{align}$

が得られる。

ii)

Pythonのプログラムによって求める。

n = 30
x = 9
y = 12
z = 4
u = 5

before_correction = n * (x * u - y * z)**2 / ((x + z) * (y + u) * (x + y) * (z + u))
after_correction = n * (x * u - y * z + n / 2)**2 / ((x + z) * (y + u) * (x + y) * (z + u))

print("Before correction: {}, After correction: {}".format(before_correction, after_correction))

上記のプログラムを実行すると、

Before correction: 0.006464124111182934, After correction: 0.10342598577892695

が得られる。

12.9

$\begin{align} Z = \frac{ \hat{p_{1}} - \hat{p_{2}} } { \sqrt{ (1/n_{1} + 1/n_{2}) \hat{p} (1 - \hat{p}) } } \end{align}$

が標準正規分布に従うから、

$\begin{align} -Z_{0.025} \le Z = \frac{\hat{p_{1}} - \hat{p_{2}}}{\sqrt{ (1/n_{1} + 1/n_{2}) \hat{p} (1 - \hat{p}) } } \le Z_{0.025} \end{align}$

を満たすとき、有意水準5%で男女に知能検査の合格率の差がないと言える。

これをPythonのプログラムによって求める。

from math import sqrt
from scipy.stats import norm

n1 = 102
n2 = 101
p1 = 18 / n1
p2 = 8 / n2
p = 26 / (n1+n2)

criteria = (p1 - p2) / sqrt((1/n1 + 1/n2) * p * (1 - p))
rejection = norm.ppf(q=1-0.025, loc=0, scale=1)

print("Rejection: |z| > |{}|, Criteria: {}, {}".format(rejection, criteria, "Equal" if abs(criteria) < abs(rejection) else "Not equal"))

上記のプログラムを実行すると、

Rejection: |z| > |1.959963984540054|, Criteria: 2.073393155507257, Not equal

が得られ、男女に知能検査の合格率の差があると言える。

12.10

3.1 より、標本相関係数 $r_{XY}$ は、 $r_{XY} = 0.6387815655787518$ である。

z変換、

$\begin{align} z = \frac{1}{2} \log \frac{1+r}{1-r} \end{align}$

$\begin{align} \eta = \frac{1}{2} \log \frac{1 + \rho}{1 - \rho} \end{align}$

より、 $\sqrt{n-3} (z - \eta)$ が標準正規分布に従うことから、

$\begin{align} -Z_{0.025} \le \sqrt{n-3} (z - \eta) \le Z_{0.025} \end{align}$

有意水準5%で帰無仮説が成り立つと言える。

これをPythonプログラムで確認する。

from math import sqrt, log
from scipy.stats import norm

r = 0.6387815655787518
z = log((1+r) / (1-r)) / 2
n = 47

rejection = norm.ppf(q=1-0.025, loc=0, scale=1)

no_str = ["i)", "ii)"]
for i, rho in enumerate([0, 0.5]):
    eta = log((1+rho) / (1-rho)) / 2
    criteria = sqrt(n - 3) * (z - eta)
    print("{} Rejection: |z| > |{}|, Criteria: {}, {}".format(no_str[i], rejection, criteria, "Accept" if abs(criteria) < abs(rejection) else "Reject"))

上記のプログラムを実行すると、

i) Rejection: |z| > |1.959963984540054|, Criteria: 5.015484383021951, Reject
ii) Rejection: |z| > |1.959963984540054|, Criteria: 1.3717996314362153, Accept

となり、i)の $H_{0} : \rho = 0$ は棄却され、ii) の $H_{0} : \rho = 0.5$ は棄却されない。

2020-10-05

【統計学入門（東京大学出版会）】第11章練習問題解答

統計学

東京大学出版会から出版されている統計学入門（基礎統計学Ⅰ）について第11章の練習問題の解答を書いていく。

本章以外の解答
11.1
11.2
11.3
11.4
11.5
11.6
11.7
- i)
- ii)
- iii)
11.8
11.9

本章以外の解答

本章以外の練習問題の解答は別の記事で公開している。
必要に応じて参照されたい。

11.1

指数分布 $E_{x} (\lambda)$ は次のように与えられる。

$\begin{align} E_{x} (\lambda) = \lambda e^{-\lambda x} \end{align}$

ここから得られる大きさ $n$ の標本 $L (\lambda)$ は、

$\begin{align} L (\lambda) &= \prod_{i=1}^{n} E\_{xi} (\lambda) \\ &= \prod_{i=1}^{n} \lambda e^{-\lambda x_{i}} \end{align}$

であるから、 $\lambda$ の最尤推定量は、

$\begin{align} \frac{d}{d\lambda} \log L(\lambda) &= \frac{d}{d\lambda} \left( n \log \lambda - \lambda \sum_{i}^{n} x_{i} \right) \\ &= \frac{n}{\lambda} - \sum_{i}^{n} x_{i} \\ &= \frac{n}{\lambda} - n \cdot \bar{X} \\ &= 0 \end{align}$

より、

$\begin{align} \lambda = \frac{1}{\bar{X}} \end{align}$

と求まる。

11.2

$X_{1}, X_{2}$ の線型推定量であるから、求める推定量は $Y = aX_{1} + bX_{2}$ である。またこれは不偏性を満たすことを利用すると、求める推定量が $\hat{\mu} = aX_{1} + bX_{2}$ となるように $a, b$ の値を決められる。したがって、

$\begin{align} E(\hat{\mu}) &= E(aX_{1} + bX_{2}) \\ &= aE(X_{1}) + bE(X_{2}) \\ &= a\mu + b\mu \\ &= \mu \end{align}$

より、 $a + b = 1$ の条件を得る。

また正規母集団の分散を $\sigma^{2}$ とすると、 $\hat{\mu}$ の分散は、

$\begin{align} V(aX_{1} + bX_{2}) &= a^{2}V(X_{1}) + b^{2}V(X_{2}) \\ &= a^{2} \sigma^{2} + b^{2} \sigma^{2} \\ &= (2a^{2} - 2a + 1) \sigma^{2} \end{align}$

となるから、この分散を最小とする $a$ は、

$\begin{align} \frac{dV}{da} &= (4a - 2) \sigma^{2} \\ &= 0 \end{align}$

より、

$\begin{align} a = \frac{1}{2}, b = \frac{1}{2} \end{align}$

であるから、分散の最小の推定量は $\frac{1}{2} \sigma^{2}$ となる。

11.3

標本平均 $\bar{X}$ は、

$\begin{align} \bar{X} &= \frac{9.75 + 7.95 + 12.8 + 8.25 + 9.86}{5} \\ &= 9.722 \end{align}$

である。

標準化

$\begin{align} z = \frac{\bar{X} - \mu}{\sqrt{\sigma^{2} / n}} \end{align}$

を行うと、その信頼係数95%の信頼区間は、

$\begin{align} P \left( - z_{0.025} \le z \le z_{0.025} \right) &= P \left( - z_{0.025} \le \frac{\bar{X} - \mu}{\sigma^{2} / n} \le z_{0.025} \right) \\ &= P \left( - z_{0.025} \le \frac{\bar{X} - \mu}{4 / 5} \le z_{0.025} \right) \\ &= P \left( -\sqrt{\frac{4}{5}} z_{0.025} + 9.722 \le \mu \le \sqrt{\frac{4}{5}} z_{0.025} + 9.722 \right) \end{align}$

と表せる。これを次のPythonプログラムを用いて求める。

from scipy.stats import norm
from math import sqrt

x1 = -sqrt(4/5) * norm.ppf(q=1-0.025, loc=0, scale=1) + 9.722
x2 = sqrt(4/5) * norm.ppf(q=1-0.025, loc=0, scale=1) + 9.722

print(f"{x1} <= u <= {x2}")

プログラムを実行すると、母平均 $\mu$ の95%信頼区間、

7.968954918846837 <= u <= 11.475045081153162

が得られる。

11.4

標本平均を $\bar{X}$ とする。

$\begin{align} z = \frac{\bar{X} - \mu}{\sqrt{\sigma^{2} / n}} \end{align}$

を行うと、その信頼係数99%の信頼区間は、

$\begin{align} P \left( - z_{0.005} \le z \le z_{0.005} \right) &= P \left( - z_{0.005} \le \frac{\bar{X} - \mu}{\sigma^{2} / n} \le z_{0.005} \right) \\ &= P \left( -\sqrt{\frac{\sigma^{2}}{n}} z_{0.005} + \bar{X} \le \mu \le \sqrt{\frac{\sigma^{2}}{n}} z_{0.005} + \bar{X} \right) \end{align}$

で表され、その幅が1以下であるという条件より、

$\begin{align} \left( \sqrt{\frac{\sigma^{2}}{n}} z_{0.005} + \bar{X} \right) - \left( -\sqrt{\frac{\sigma^{2}}{n}} z_{0.005} + \bar{X} \right) &= 2 \sqrt{\frac{\sigma^{2}}{n}} z_{0.005} \\ &\le 1 \end{align}$

が得られ、 $n$ の条件は、

$\begin{align} n &\ge \left( 2 \sigma z_{0.005} \right)^{2} \\ &= 36 z_{0.005}^{2} \end{align}$

で表される。ここから、Pythonプログラム

from scipy.stats import norm

x = 36 * norm.ppf(q=1-0.005, loc=0, scale=1)**2

print(f"n >= {x}")

によって、

n >= 238.85627763676368

が得られるため、 $n$ は 239以上となる必要がある。

11.5

投薬群の標本平均を $\bar{X_{1}}$ 、標本分散を $s_{1}^{2}$ 、母平均を $\mu_{1}$ 、標本数を $m$ とする。
また、対照群の標本平均を $\bar{X_{2}}$ 、標本分散を $s_{2}^{2}$ 、母平均を $\mu_{2}$ 、標本数を $n$ とする。

母分散が等しいと考えられるため、

$\begin{align} t = \frac{(\bar{X_{1}} - \bar{X_{2}}) - (\mu_{1} - \mu_{2})}{s \sqrt{\frac{1}{m} + \frac{1}{n}}} \end{align}$

は自由度 $m + n - 2$ のスチューデントのt分布に従う。

これを用いると $\mu_{1} - \mu_{2}$ の95%信頼区間は、

$\begin{align} P \left( -t_{0.025} \le \frac{(\bar{X_{1}} - \bar{X_{2}}) - (\mu_{1} - \mu_{2})}{s \sqrt{\frac{1}{m} + \frac{1}{n}}} \le t_{0.025} \right) &= P \left( -t_{0.025} s \sqrt{\frac{1}{m} + \frac{1}{n}} + (\bar{X} + \bar{Y}) \le \mu_{1} - \mu_{2} \le t_{0.025} s \sqrt{\frac{1}{m} + \frac{1}{n}} + (\bar{X} + \bar{Y}) \right) \end{align}$

となる。

上記を求めるPythonプログラムを次に示す。

import numpy as np
from scipy.stats import t
from math import sqrt

x1 = np.array([7.97, 7.66, 7.59, 8.44, 8.05, 8.08, 8.35, 7.77, 7.98, 8.15])
x2 = np.array([8.06, 8.27, 8.45, 8.05, 8.51, 8.14, 8.09, 8.15, 8.16, 8.42])
x1_bar = x1.mean()
x2_bar = x2.mean()
m = x1.size
n = x2.size
s = sqrt((np.sum((x1 - x1_bar)**2) + np.sum((x2 - x2_bar)**2)) / (m + n - 2))
t_val = t.ppf(q=1-0.025, df=m+n-2)

print("{} <= u1 - u2 <= {}".format(
    -t_val * s * sqrt(1/m + 1/n) + (x1_bar - x2_bar),
    t_val * s * sqrt(1/m + 1/n) + (x1_bar - x2_bar)
))

プログラムを実行すると次の結果が得られる。

-0.44185376487974576 <= u1 - u2 <= -0.010146235120252423

11.6

母分散が等しくないと考えられるため、ウェルチの近似法を利用する。

標準法の標本平均を $\bar{X_{1}}$ 、標本分散を $s_{1}^{2}$ 、母平均を $\mu_{1}$ 、標本数を $m$ とする。
また、簡便法の標本平均を $\bar{X_{2}}$ 、標本分散を $s_{2}^{2}$ 、母平均を $\mu_{2}$ 、標本数を $n$ とする。

このとき、自由度が

$\begin{align} \nu = \frac{ \left( \frac{s_{1}^{2}}{m} + \frac{s_{2}^{2}}{n} \right)^{2} }{ \frac{ \left( s_{1}^{2} / m \right)^{2} }{m - 1} + \frac{ \left( s_{2}^{2} / n \right)^{2} }{n - 1} } \end{align}$

に最も近い整数としたときに、

$\begin{align} t = \frac{(\bar{X_{1}} - \bar{X_{2}}) - (\mu_{1} - \mu_{2})}{\sqrt{\frac{s_{1}^{2}}{m} + \frac{s_{2}^{2}}{n}}} \end{align}$

で表されるスチューデントのt分布に従う。

これを用いると $\mu_{1} - \mu_{2}$ の95%信頼区間は、

$\begin{align} P \left( -t_{0.025} \le \frac{(\bar{X_{1}} - \bar{X_{2}}) - (\mu_{1} - \mu_{2})}{\sqrt{\frac{s_{1}^{2}}{m} + \frac{s_{2}^{2}}{n}}} \le t_{0.025} \right) &= P \left( -t_{0.025} \sqrt{\frac{s_{1}^{2}}{m} + \frac{s_{2}^{2}}{n}} + (\bar{X} + \bar{Y}) \le \mu_{1} - \mu_{2} \le t_{0.025} \sqrt{\frac{s_{1}^{2}}{m} + \frac{s_{2}^{2}}{n}} + (\bar{X} + \bar{Y}) \right) \end{align}$

となる。

これをPythonプログラム

import numpy as np
from scipy.stats import t
from math import sqrt
from decimal import Decimal, ROUND_HALF_UP

x1 = np.array([25, 24, 25, 26])
x2 = np.array([23, 18, 22, 28, 17, 25, 19, 16])
x1_bar = x1.mean()
x2_bar = x2.mean()
m = x1.size
n = x2.size
s21 = np.sum((x1 - x1_bar)**2) / (m - 1)
s22 = np.sum((x2 - x2_bar)**2) / (n - 1)
s = sqrt((np.sum((x1 - x1_bar)**2) + np.sum((x2 - x2_bar)**2)) / (m + n - 2))
nu = (s21/m + s22/n)**2 / ((s21/m)**2/(m-1) + (s22/n)**2/(n-1))
nu = int(Decimal(str(nu)).quantize(Decimal('0'), rounding=ROUND_HALF_UP))
t_val = t.ppf(q=1-0.025, df=nu)

print(f"nu: {nu}")
print("{} <= u1 - u2 <= {}".format(
    -t_val * sqrt(s21/m + s22/n) + (x1_bar - x2_bar),
    t_val * sqrt(s21/m + s22/n) + (x1_bar - x2_bar)
))

によって求めると、

nu: 8
0.4417583693791478 <= u1 - u2 <= 7.558241630620852

が得られる。

11.7

i)

標本平均を $\bar{X}$ 、標本分散を $s^{2}$ 、母平均を $\mu$ 、標本数を $n$ としたとき、

$\begin{align} t = \frac{\bar{X} - \mu}{\sqrt{s^{2}/n}} \end{align}$

が自由度 $n - 1$ のスチューデントのt分布に従う。

ここから母平均 $\mu$ の99%信頼区間は、

$\begin{align} &P \left( -t_{0.025} \le \frac{\bar{X} - \mu}{\sqrt{s^{2}/n}} \le t_{0.025} \right) \\ &= P \left( -t_{0.025} \sqrt{\frac{s^{2}}{n}} + \bar{X} \le \mu \le t_{0.025} \sqrt{\frac{s^{2}}{n}} + \bar{X} \right) \end{align}$

を求めればよい。

これを求めるPythonプログラムは次のようになる。

import numpy as np
from scipy.stats import t
from math import sqrt

x = np.array([21.8, 22.4, 22.7, 24.5, 25.9, 24.9, 24.8, 25.3, 25.2, 24.6])
x_bar = x.mean()
n = x.size
s2 = np.sum((x - x_bar)**2)/(n-1)
t_val = t.ppf(q=1 - 0.005, df=n-1)

print("{} <= u <= {}".format(
    -sqrt(s2/n) * t_val + x_bar,
    sqrt(s2/n) * t_val + x_bar
))

上記のプログラムを実行すると、

22.779046896409294 <= u <= 25.640953103590707

が得られる。

ii)

母分散を $\sigma^{2}$ 、標本分散を $s^{2}$ 、標本数を $n$ としたとき、

$\begin{align} \chi^{2} = \frac{(n-1)s^{2}}{\sigma^{2}} \end{align}$

が自由度 $n - 1$ の $\chi^{2}$ 分布に従う。

ここから、母分散 $\sigma^{2}$ の95%信頼区間は、

$\begin{align} &P \left( \chi_{0.975}^{2} \le \frac{(n-1)s^{2}}{\sigma^{2}} \le \chi_{0.025}^{2} \right) \\ &= P \left( \frac{s^{2}(n-1)}{\chi_{0.025}^{2}} \le \sigma^{2} \le \frac{s^{2}(n-1)}{\chi_{0.975}^{2}} \right) \end{align}$

を求めればよい。

これを求めるPythonプログラムは次のようになる。

import numpy as np
from scipy.stats import chi2

x = np.array([21.8, 22.4, 22.7, 24.5, 25.9, 24.9, 24.8, 25.3, 25.2, 24.6])
x_bar = x.mean()
n = x.size
s2 = np.sum((x - x_bar)**2)/(n-1)
chi2_val_1 = chi2.ppf(q=1-0.025, df=n-1)
chi2_val_2 = chi2.ppf(q=1-0.975, df=n-1)

print("{} <= sigma2 <= {}".format(
    s2 * (n-1) / chi2_val_1,
    s2 * (n-1) / chi2_val_2
))

上記のプログラムを実行すると次の結果が得られる。

0.9172692525451521 <= sigma2 <= 6.461660438291186

iii)

東京の最低気温の標本平均を $\bar{X_{1}}$ 、標本分散を $s_{1}^{2}$ 、母平均を $\mu_{1}$ 、標本数を $m$ とする。
また、大阪の最低気温の標本平均を $\bar{X_{2}}$ 、標本分散を $s_{2}^{2}$ 、母平均を $\mu_{2}$ 、標本数を $n$ とする。

母集団が等しいと仮定すると、

$\begin{align} f = \frac{\bar{X} - \bar{Y}}{\sqrt{s_{1}^{2}/m + s_{2}^{2}/n}} \end{align}$

は自由度 $m + n - 2$ のスチューデントのt分布に従う。

したがって $\mu_{1} - \mu_{2}$ の95%信頼区間は、

$\begin{align} &P \left( -t_{0.025} \le \frac{\bar{X} - \bar{Y}}{\sqrt{s_{1}^{2}/m + s_{2}^{2}/n}} \le t_{0.025} \right) \\ &= \left( -t_{0.025} \sqrt{s_{1}^{2}/m + s_{2}^{2}/n} + (\bar{X} - \bar{Y}) \le \mu_{1} - \mu_{2} \le t_{0.025} \sqrt{s_{1}^{2}/m + s_{2}^{2}/n} + (\bar{X} - \bar{Y}) \right) \end{align}$

を求めればよい。

これを求めるPythonプログラムは次のようになる。

import numpy as np
from scipy.stats import t
from math import sqrt

x1 = np.array([21.8, 22.4, 22.7, 24.5, 25.9, 24.9, 24.8, 25.3, 25.2, 24.6])
x2 = np.array([22.1, 25.3, 23.3, 25.2, 25.3, 24.9, 24.9, 24.9, 24.9, 24.0])
x1_bar = x1.mean()
x2_bar = x2.mean()
m = x1.size
n = x2.size
s21 = np.sum((x1 - x1_bar)**2) / (m - 1)
s22 = np.sum((x2 - x2_bar)**2) / (n - 1)
t_val = t.ppf(q=1-0.025, df=m+n-2)

print("{} <= u1 - u2 <= {}".format(
    -t_val * sqrt(s21/m + s22/n) + (x1_bar - x2_bar),
    t_val * sqrt(s21/m + s22/n) + (x1_bar - x2_bar)
))

上記のプログラムを実行すると次の結果が得られる。

-1.4272035915681638 <= u1 - u2 <= 0.8872035915681646

11.8

標本数が $n = 50$ であるため、中心極限定理が使える。このとき二項母集団の標本平均は正規分布に従うから、標準化を行うことで標準正規分布に従うことがわかる。

なお、二項母集団 $Bi(n, p)$ の平均と分散は次の式で表される。

$E(x) = np \\ V(x) = np(1-p)$

したがって、 $p$ の95%信頼区間は、

$\begin{align} &P \left( -z_{0.025} \le \frac{\bar{X} - np}{\sqrt{np(1-p)}} \le z_{0.025} \right) \\ &= P \left( \bar{X} - z_{0.025} \sqrt{\frac{\bar{X} ( 1 - \bar{X} ) }{n}} \le p \le \bar{X} + z_{0.025} \sqrt{\frac{\bar{X} ( 1 - \bar{X} ) }{n}} \right) \end{align}$

を求めることができる。ここで、 $\bar{X}$ は標本平均、 $n$ は標本数とした。

Pythonプログラム

from scipy.stats import norm
from math import sqrt

x_bar = 27 / 50
n = 50
z_val = norm.ppf(q=1-0.025, loc=0, scale=1)

print("{} <= p <= {}".format(
    x_bar - z_val * sqrt(x_bar * (1 - x_bar) / n),
    x_bar + z_val * sqrt(x_bar * (1 - x_bar) / n)
))

を実行することで、

0.4018538186513706 <= p <= 0.6781461813486295

を得る。

11.9

中心極限定理が使う。このときポアソン母集団の標本平均は正規分布に従うから、標準化を行うことで標準正規分布に従うことがわかる。

ポアソン分布は再生性により、標本数 $n$ のときに $Po(n\lambda)$ に従う。したがってこの平均と分散は次の式で表される。

$E(x) = n\lambda \\ V(x) = n\lambda$

したがって、 $\lambda$ の99%信頼区間は、

$\begin{align} &P \left( -z_{0.005} \le \frac{\bar{X} - n\lambda}{\sqrt{n\lambda}} \le z_{0.005} \right) \\ &= P \left( \bar{X} - z_{0.005} \sqrt{\frac{\bar{X}}{n}} \le \lambda \le \bar{X} + z_{0.005} \sqrt{\frac{\bar{X}}{n}} \right) \end{align}$

を求めることができる。ここで、 $\bar{X}$ は標本平均、 $n$ は標本数とした。

Pythonプログラム

import numpy as np
from scipy.stats import norm
from math import sqrt

x = np.array([4, 3, 5, 4, 8, 2, 5, 9, 3, 5])
x_bar = x.mean()
n = x.size
z_val = norm.ppf(q=1-0.005, loc=0, scale=1)
print("{} <= lambda <= {}".format(
    x_bar - z_val * sqrt(x_bar / n),
    x_bar + z_val * sqrt(x_bar / n)
))

を実行することで、

3.015413109851419 <= lambda <= 6.5845868901485805

を得る。